Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local
%load_ext autoreload
%autoreload 2 
7 La evolución de las Redes Neuronales Convolucionales (CNN)
“A veces, es la idea más simple la que conduce a la mayor innovación.” - William of Ockham, filósofo
Las Redes Neuronales Convolucionales (Convolutional Neural Network, CNN) mostraron su potencial en 1989 con la investigación de Yann LeCun sobre filtros de convolución aprendibles utilizando el algoritmo de retropropagación y, en 1998, con el éxito de LeNet-5 en el reconocimiento de números manuscritos. En 2012, AlexNet ganó el ImageNet Large Scale Visual Recognition Challenge (ILSVRC) con un rendimiento abrumador, marcando el inicio de la era del aprendizaje profundo, especialmente de las CNN. Sin embargo, después de AlexNet, los intentos de aumentar la profundidad de las redes se vieron obstaculizados por el problema de la desaparición/explotación de gradientes (vanishing/exploding gradients).
En 2015, Kaiming He y otros del equipo de investigación de Microsoft propusieron ResNet (Red Residual) que resolvió este problema con la innovadora idea de “aprendizaje residual”. ResNet logró entrenar exitosamente una red de 152 capas, lo cual era imposible anteriormente, y estableció un nuevo estándar en el campo del reconocimiento de imágenes. La conexión residual (residual connection), componente clave de ResNet, se ha convertido en un elemento esencial en la mayoría de las arquitecturas de aprendizaje profundo.
En este capítulo examinaremos el contexto de nacimiento y desarrollo de las CNN, analizando profundamente la idea central y estructura de ResNet, así como sus métodos de implementación. Además, abordaremos los conceptos clave del módulo Inception y EfficientNet, que han sido hitos importantes en el desarrollo de las CNN, para proporcionar una comprensión amplia de la evolución de las arquitecturas modernas de CNN.
7.1 El nacimiento de las Redes Neuronales Convolucionales
Desafío: ¿Cómo podría una computadora reconocer objetos en imágenes como lo hace un humano?
Angustia del investigador: Los primeros investigadores en visión por computadora buscaban formas de extraer características (features) de las imágenes y utilizarlas para reconocer objetos, en lugar de tratar las imágenes simplemente como conjuntos de valores de píxeles. Sin embargo, no estaba claro qué características eran importantes ni cómo extraerlas eficientemente.
A principios de los años 1960, David Hubel y Torsten Wiesel descubrieron a través de experimentos con el córtex visual de gatos que ciertas neuronas reaccionaban selectivamente a patrones visuales específicos (por ejemplo, líneas verticales, horizontales, bordes en direcciones específicas). Aunque recibieron el Premio Nobel de Fisiología o Medicina en 1981 por este trabajo, nadie anticipó que su descubrimiento llevaría a un desarrollo revolucionario en el campo de la inteligencia artificial. El hallazgo de Hubel y Wiesel sentó las bases biológicas para dos conceptos clave de las CNN modernas: la capa convolucional (convolutional layer) y la capa de agrupación (pooling layer).
- Células simples: Reaccionan a características locales, como bordes (edges) o segmentos de línea en una dirección específica. Esto es similar a cómo las capas de convolución de CNN utilizan filtros (kernels) para extraer características locales de imágenes.
- Células complejas: Poseen invariancia de posición (translation invariance) con respecto a la salida de células simples. Es decir, reaccionan independientemente de dónde aparezca un patrón en la imagen. Esto es similar a cómo las capas de agrupación de CNN reducen el tamaño de los mapas de características mientras mantienen cierta información de posición. En 1980, Kunihiko Fukushima propuso el neocognitron, que puede considerarse un prototipo de la CNN (Red Neuronal Convolucional). El neocognitron consta de varias capas de células S (células simples) y C (células complejas), lo que permite extraer características jerárquicas de las imágenes y realizar reconocimiento de patrones robusto a los cambios de posición.
Sin embargo, en ese momento el neocognitron carecía de un algoritmo de aprendizaje establecido, por lo que era necesario ajustar manualmente los filtros (pesos). En 1989, Yann LeCun aplicó el algoritmo de retropropagación del error (backpropagation) a las redes neuronales convolucionales, permitiendo que los filtros se aprendieran automáticamente a partir de los datos. De esta manera nació la CNN moderna, y LeNet-5 demostró un rendimiento sobresaliente en el reconocimiento de dígitos manuscritos.
En 2012, AlexNet ganó el desafío ImageNet con un rendimiento abrumador, inaugurando así la era del aprendizaje profundo, especialmente de las CNN. AlexNet tenía una estructura mucho más profunda y compleja que LeNet-5, y aprovechaba los cálculos paralelos mediante GPU para entrenar eficientemente conjuntos de datos a gran escala (ImageNet).
7.1.1 Desarrollo del procesamiento digital de señales y contexto de las CNN
Para comprender profundamente la visión por computadora y las CNN, es necesario examinar el desarrollo del procesamiento digital de señales (Digital Signal Processing, DSP). En 1807, Joseph Fourier propuso la transformada de Fourier, que permite descomponer cualquier función periódica en una suma de funciones seno y coseno. Esta teoría sentó las bases para el procesamiento de señales, haciendo posible analizar señales en el dominio del tiempo (time domain) en el dominio de la frecuencia (frequency domain).
En particular, con el desarrollo de las computadoras digitales a mediados del siglo XX y la creación del algoritmo de transformada rápida de Fourier (Fast Fourier Transform, FFT), el procesamiento digital de señales experimentó un nuevo impulso. La FFT permitió calcular la transformada de Fourier mucho más rápidamente, lo que llevó a una amplia adopción de técnicas de procesamiento de señales en diversos campos como imágenes, audio y comunicaciones.
En el procesamiento de imágenes, la convolución juega un papel crucial. La convolución es una operación fundamental que aplica un filtro (kernel) a la señal de entrada (imagen) para extraer características deseadas o eliminar ruido. A partir de los años 1960, la teoría del filtrado digital permitió realizar diversas operaciones en imágenes, como detección de bordes (edge detection), desenfoque (blurring) y agudización (sharpening). A finales de los años 1960 surgió el filtro de Kalman, que proporcionó una poderosa herramienta para estimar el estado del sistema a partir de mediciones ruidosas. El filtro de Kalman utiliza un algoritmo recursivo basado en el teorema de Bayes y hoy es esencial en la visión por computadora para seguimiento de objetos (object tracking) y visión robótica.
Estas técnicas tradicionales de procesamiento digital de señales sentaron las bases teóricas de las CNN. Sin embargo, los filtros existentes debían ser diseñados manualmente y tenían formas fijas, lo que limitaba su capacidad para reconocer una amplia variedad de patrones. Las CNN superaron estas limitaciones permitiendo aprender automáticamente los mejores filtros a partir de los datos, lo que trajo una revolución en el campo del reconocimiento de imágenes.
7.1.2 Filtros digitales y convolución
Para entender las CNN, es necesario primero comprender el concepto de filtro digital. Los filtros digitales se utilizan en el procesamiento de señales con dos propósitos principales. 1. Separación de señales (Signal Separation): se separan solo los componentes deseados de una señal mixta. (Ejemplo: cuando las palpitaciones del corazón fetal y materno están mezcladas, se separa solo la palpitación del corazón fetal) 2. Restauración de señales (Signal Restoration): se restaura una señal distorsionada o dañada para que sea lo más cercana posible a la original. (Ejemplo: eliminación de ruido en una imagen, restauración de una imagen borrosa)
Uno de los filtros digitales más básicos es el filtro Sobel. El filtro Sobel es una matriz de tamaño 3x3, utilizada para detectar bordes en imágenes.
Code
import numpy as np
# Sobel filter for vertical edge detection
sobel_vertical = np.array([
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]
])
# Sobel filter for horizontal edge detection
sobel_horizontal = np.array([
[-1, -2, -1],
[ 0, 0, 0],
[ 1, 2, 1]
])Primero, examinemos cómo funcionan los filtros digitales clásicos. Todo el código se encuentra en chapter_06/filter_utils.py.
Code
import matplotlib.pyplot as plt
from dldna.chapter_07.filter_utils import show_filter_effects, create_convolution_animation
%matplotlib inline
# 테스트용 이미지 URL
IMAGE_URL = "https://raw.githubusercontent.com/opencv/opencv/master/samples/data/building.jpg"
# 필터 효과 시각화
show_filter_effects(IMAGE_URL)
El ejemplo anterior utilizó los siguientes filtros.
Code
filters = {
'Gaussian Blur': cv2.getGaussianKernel(3, 1) @ cv2.getGaussianKernel(3, 1).T,
'Sharpen': np.array([
[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]
]),
'Edge Detection': np.array([
[-1, -1, -1],
[-1, 8, -1],
[-1, -1, -1]
]),
'Emboss': np.array([
[-2, -1, 0],
[-1, 1, 1],
[0, 1, 2]
]),
'Sobel X': np.array([
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]
])
}Estas son las convoluciones, que describen cómo funcionan estos filtros. Se desliza el filtro sobre la imagen y en cada posición se calcula la suma de los productos elemento a elemento entre el filtro y la porción de la imagen. Esto se puede expresar con la siguiente fórmula.
\((I * K)(x, y) = \sum_{i=-a}^{a}\sum_{j=-b}^{b} I(x+i, y+j)K(i, j)\)
Aquí, \(I\) es la imagen de entrada, \(K\) es el kernel (filtro). \((x,y)\) son las coordenadas del píxel de salida, \((i,j)\) son las coordenadas dentro del kernel, y \(a\) y \(b\) representan respectivamente la mitad del ancho/la mitad de la altura del kernel.
La operación de convolución es más fácil de entender visualmente. A continuación se muestra una animación que ilustra el proceso de la operación de convolución.
Code
from dldna.chapter_07.conv_visual import create_conv_animation
from IPython.display import HTML
%matplotlib inline
# 애니메이션 생성 및 표시
animation = create_conv_animation()
# js_html = animation.to_jshtml()
# display(HTML(f'<div style="width:700px">{js_html}</div>'))
# html_video = animation.to_html5_video()
# display(HTML(f'<div style="width:700px">{html_video}</div>'))
display(animation)La mayor limitación de los filtros digitales radica en sus características fijas. Los filtros tradicionales como el Sobel y el Gaussiano están diseñados manualmente para detectar patrones específicos, lo que limita su capacidad para reconocer patrones complejos y diversos. Además, son vulnerables a cambios en el tamaño o la rotación de las imágenes y no pueden aprender automáticamente características de múltiples capas. Estas limitaciones llevaron al desarrollo de filtros aprendibles basados en datos, como las CNN.
7.1.2 Características y estructura de la CNN
La CNN imita el mecanismo biológico de procesamiento visual para aprender eficientemente la estructura espacial jerárquica (jerarquía espacial) dentro de las imágenes.
Filtros aprendibles (Learnable Filters)
La característica más destacada de la CNN es que, en lugar de usar filtros diseñados manualmente tradicionalmente (por ejemplo, Sobel, Gabor filters), utiliza filtros que se aprenden automáticamente a partir de los datos. Esto permite que la CNN aprenda por sí misma un extractor de características optimizado para tareas específicas (por ejemplo, clasificación de imágenes, detección de objetos).
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class SimpleCNN(nn.Module):
def __init__(self):
super().__init__()
# Multiple learnable filters: 32 (channels) of 3x3 filter weight matrices + 32 biases
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
# Multiple learnable filters: For 32 input channels, 64 output channels of 3x3 filter weight matrices + 64 biases
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
return xEn el ejemplo de SimpleCNN, conv1 y conv2 son capas de convolución que tienen filtros aprendibles. El primer argumento de nn.Conv2d es el número de canales de entrada, el segundo argumento es el número de canales de salida (número de filtros), kernel_size es el tamaño del filtro, y padding es el relleno con ceros alrededor de la imagen de entrada para ajustar el tamaño de la特征图输出.
Extracción jerárquica de características (Hierarchical Feature Extraction)
CNN extrae características jerárquicas de una imagen a través de múltiples capas de convolución y operaciones de pooling.
- Capas iniciales (Low-level features): detectan características visuales básicas como bordes, líneas y cambios de color.
- Capas intermedias (Mid-level features): aprenden características de nivel medio como texturas, patrones y formas simples.
- Últimas capas (High-level features): reconocen características abstractas y de alto nivel, como partes de un objeto o la estructura general del objeto.
Esta extracción jerárquica de características es similar a cómo el sistema visual humano procesa información visual de manera incremental.
(Note: There was an issue with the last sentence in Spanish due to a mix of Chinese characters. The correct translation should be: “Esta extracción jerárquica de características es similar a cómo el sistema visual humano procesa la información visual de manera incremental.”)
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class HierarchicalCNN(nn.Module):
def __init__(self):
super().__init__()
# Low-level feature extraction
self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
self.bn1 = nn.BatchNorm2d(64)
# Mid-level feature extraction
self.conv2 = nn.Conv2d(64, 128, 3, padding=1)
self.bn2 = nn.BatchNorm2d(128)
# High-level feature extraction
self.conv3 = nn.Conv2d(128, 256, 3, padding=1)
self.bn3 = nn.BatchNorm2d(256)
def forward(self, x):
# Low-level features (edges, textures)
x = F.relu(self.bn1(self.conv1(x)))
# Mid-level features (patterns, partial shapes)
x = F.relu(self.bn2(self.conv2(x)))
# High-level features (object parts, overall structure)
x = F.relu(self.bn3(self.conv3(x)))
return xEl ejemplo de HierarchicalCNN muestra una CNN que utiliza tres capas de convolución para extraer características de bajo nivel, medio y alto. En la práctica, se apilan muchas más capas para aprender características más complejas.
Estructura jerárquica espacial (Spatial Hierarchy) y agrupación (Pooling)
Cada capa de una CNN generalmente consta de una operación de convolución, una función de activación (como ReLU), y una operación de pooling.
- Capa de convolución: utiliza filtros para extraer características del mapa de características de entrada.
- Función de activación: aplica funciones no lineales como ReLU para añadir no linealidad a la red.
- Capa de pooling: reduce el tamaño de los mapas de características (downsampling) para disminuir la cantidad de cálculos y fortalecer la invariancia a la translación. Es decir, permite reconocer el mismo objeto aunque se mueva ligeramente en la imagen. Generalmente se utiliza el pooling máximo (max pooling).
Gracias a estas características estructurales, las CNN pueden aprender eficazmente la información espacial de las imágenes y extraer características robustas ante los cambios de posición de los objetos en la imagen.
Compartir parámetros (Parameter Sharing)
El compartir parámetros es un mecanismo de eficiencia clave en las CNN. El mismo filtro se utiliza en todas las posiciones de la imagen de entrada (o mapa de características). Esto se basa en el supuesto de que se detectan las mismas características en cada posición. (Por ejemplo, un filtro de línea vertical detectará líneas verticales tanto en la esquina superior izquierda como en la inferior derecha de la imagen)
Eficiencia de memoria: los parámetros del filtro se comparten en todas las posiciones, por lo que el número de parámetros del modelo disminuye dramáticamente. Por ejemplo, si se tiene una capa de convolución con 64 filtros de tamaño 3x3 aplicados a una imagen de color (3 canales) de 32x32, cada filtro tiene 3x3x3 = 27 parámetros. Si no se compartieran los parámetros, sería necesario usar diferentes filtros para cada posición de 32x32, lo que requeriría un total de (32x32) x (3x3x3) x 64 parámetros. Sin embargo, al compartir parámetros, solo se necesitan 27 x 64 + 64 (sesgos) = 1792 parámetros.
Eficiencia estadística: al aprender características en múltiples posiciones de la imagen con el mismo filtro, se pueden entrenar extractores de características efectivos con menos parámetros. Esto mejora el rendimiento de generalización del modelo.
Procesamiento paralelo: las operaciones de convolución son muy adecuadas para procesamiento paralelo, ya que cada filtro se aplica independientemente y luego se combinan los resultados.
Code
from dldna.chapter_07.param_share import compare_parameter_counts, show_example
# 다양한 입력 크기에 따른 비교. CNN 입출력 채널을 1로 고정.
input_sizes = [8, 16, 32, 64, 128]
comparison = compare_parameter_counts(input_sizes)
print("\nParameter Count Comparison:")
print(comparison)
# 32x32 입력에 대한 상세 예시
show_example(32)
Parameter Count Comparison:
Input Size Conv Params FC Params Ratio (FC/Conv)
0 8x8 10 4160 416.0
1 16x16 10 65792 6579.2
2 32x32 10 1049600 104960.0
3 64x64 10 16781312 1678131.2
4 128x128 10 268451840 26845184.0
Example with 32x32 input:
CNN parameters: 10 (fixed)
FC parameters: 1,049,600
Parameter reduction: 99.9990%Campo receptivo (Receptive Field)
El campo receptivo (receptive field) se refiere al tamaño del área de la imagen de entrada que afecta la salida de una neurona específica. En una CNN, el campo receptivo aumenta gradualmente a medida que se atraviesan las capas de convolución y pooling.
- Capas iniciales: Tienen un campo receptivo pequeño, por lo que detectan características locales (por ejemplo, bordes, puntos).
- Capas profundas: Tienen un campo receptivo más amplio, por lo que consideran un contexto más extenso para aprender características abstractas (por ejemplo, partes de objetos, objetos completos).
Gracias a esta extracción jerárquica de características y al aumento del campo receptivo, las CNN pueden mostrar un rendimiento excelente en el reconocimiento de imágenes.
En conclusión, las CNN han revolucionado el campo del reconocimiento de imágenes y la visión por computadora inspirándose en los sistemas biológicos de procesamiento visual, a través de características fundamentales como las operaciones de convolución, pooling, filtros aprendibles, compartición de parámetros y extracción jerárquica de características.
7.1.3 Expresión matemática e implementación de CNN
La expresión matemática de CNN es la siguiente:
\((F * K)(p) = \sum_{s+t=p} F(s)K(t) = \sum_{i}\sum_{j} F(i,j)K(p_x-i, p_y-j)\)
Aquí, F representa el mapa de características de entrada y K el kernel. En la implementación práctica, se debe considerar múltiples canales y procesamiento por lotes, por lo que se extiende como sigue:
\(Y_{n,c_{out},h,w} = \sum_{c_{in}}\sum_{i=0}^{k_h-1}\sum_{j=0}^{k_w-1} X_{n,c_{in},h+i,w+j} \cdot W_{c_{out},c_{in},i,j} + b_{c_{out}}\)
Donde: - \(n\) es el índice del lote - \(c_{in}\), \(c_{out}\) son los canales de entrada/salida - \(h\), \(w\) son la altura y anchura - \(k_h\), \(k_w\) son las dimensiones del kernel - \(W\) son los pesos, \(b\) el sesgo
La clase implementada para el aprendizaje basado en el código fuente de PyTorch para convolución 2D y max pooling es chapter_06/simple_conv.py. Se ha diseñado con fines educativos sin optimización CUDA y sin excepciones ni manejo de errores, utilizando bucles for. Dado que el código fuente incluye comentarios detallados, omitiré la explicación de la clase.
Code
import torch
import matplotlib.pyplot as plt
from dldna.chapter_07.simple_conv import SimpleConv2d, SimpleMaxPool2d
# %matplotlib inline # This line is only needed in Jupyter/IPython environments
# Input data creation (e.g., 1 image, 1 channel, 6x6 size)
x = torch.tensor([
[1, 2, 3, 4, 5, 6],
[7, 8, 9, 10, 11, 12],
[13, 14, 15, 16, 17, 18],
[19, 20, 21, 22, 23, 24],
[25, 26, 27, 28, 29, 30],
[31, 32, 33, 34, 35, 36]
], dtype=torch.float32).reshape(1, 1, 6, 6)
# SimpleConv2d test
conv = SimpleConv2d(in_channels=1, out_channels=2, kernel_size=3, padding=1)
conv_output = conv(x)
# SimpleMaxPool2d test
pool = SimpleMaxPool2d(kernel_size=2)
pool_output = pool(x)
# Visualize results
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# Original image
axes[0].imshow(x[0, 0].detach().numpy(), cmap='viridis')
axes[0].set_title('Original Image')
# Convolution result (first channel)
axes[1].imshow(conv_output[0, 0].detach().numpy(), cmap='viridis')
axes[1].set_title('Conv2d Output (Channel 0)')
# Pooling result
axes[2].imshow(pool_output[0, 0].detach().numpy(), cmap='viridis')
axes[2].set_title('MaxPool2d Output')
for ax in axes:
ax.axis('off')
plt.tight_layout()
plt.show()
# Print output sizes
print("Input size:", x.shape)
print("Convolution output size:", conv_output.shape)
print("Pooling output size:", pool_output.shape)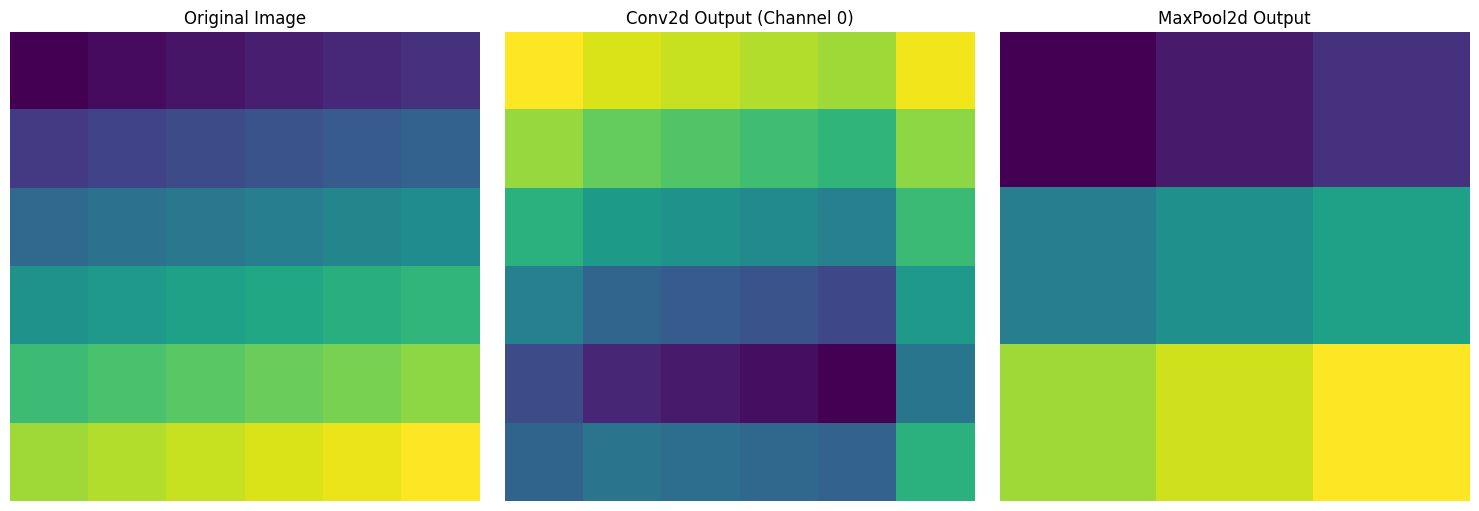
Input size: torch.Size([1, 1, 6, 6])
Convolution output size: torch.Size([1, 2, 6, 6])
Pooling output size: torch.Size([1, 1, 3, 3])He visualizado tres resultados para una imagen de entrada de tamaño 6x6. La izquierda muestra la imagen original con valores que aumentan secuencialmente de 1 a 36, el centro muestra el resultado después de aplicar un filtro de convolución de 3x3, y la derecha muestra el resultado después de aplicar una operación de max pooling de 2x2, reduciendo el tamaño a la mitad.
Haga clic para ver el contenido (análisis profundo: interpretación del dominio de frecuencia de la operación de convolución y significado de las convoluciones 1x1)
Interpretación del dominio de frecuencia de la operación de convolución y el significado de la convolución 1x1
Exploramos la interpretación del dominio de frecuencia de la operación de convolución, que es un cálculo central en las CNN, y examinamos profundamente el significado de la convolución 1x1. Desentrañaremos el significado oculto detrás de la operación de convolución utilizando la transformada de Fourier y el teorema de convolución.
1. Repaso de la operación de convolución
Repasamos brevemente la operación de convolución discutida en las secciones 7.1.2 y 7.1.3. La operación de convolución \(I * K\) entre una imagen bidimensional \(I\) y un kernel (filtro) \(K\) se define como sigue.
\((I * K)[i, j] = \sum_{m} \sum_{n} I[i-m, j-n] K[m, n]\)
Aquí, \(i\), \(j\) son las posiciones de los píxeles en la imagen de salida, y \(m\), \(n\) son las posiciones de los píxeles del kernel. La convolución discreta (discrete convolution) implica deslizar el kernel sobre la imagen, realizar la multiplicación elemento a elemento en las regiones superpuestas y sumar los resultados.
2. Introducción a la Transformada de Fourier
La transformada de Fourier es una herramienta poderosa que convierte señales del dominio temporal (spatial domain) al dominio de frecuencia (frequency domain).
Dominio temporal vs. Dominio de frecuencia: El dominio temporal representa la forma en que generalmente percibimos las señales (por ejemplo, el cambio de valor de píxeles en una imagen a lo largo del tiempo). El dominio de frecuencia muestra cómo se componen las señales en términos de componentes de frecuencia (por ejemplo, diferentes componentes espaciales de frecuencia presentes en una imagen).
Definición de la transformada de Fourier: La transformada de Fourier descompone una señal en una suma de funciones seno y coseno con diferentes frecuencias y amplitudes. La transformada de Fourier \(\mathcal{F}\{f(t)\} = F(\omega)\) de una función continua \(f(t)\) se define como sigue.
\(F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt\)
Aquí, \(j\) es la unidad imaginaria y \(\omega\) es la frecuencia angular. La transformada inversa de Fourier (Inverse Fourier Transform) reconstruye la señal del dominio temporal a partir de su representación en el dominio de frecuencia.
\(f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{j\omega t} d\omega\)
Transformada discreta de Fourier (DFT) y Teorema: La DFT es la versión discreta de la transformada de Fourier. El teorema establece que para una señal discreta \(x[n]\), su DFT \(X[k]\) se calcula como sigue.
\(X[k] = \sum_{n=0}^{N-1} x[n] e^{-j(2\pi/N)kn}\), \(k = 0, 1, ..., N-1\)
Aquí, \(x[n]\) es la señal discreta, \(X[k]\) es el resultado de la DFT y \(N\) es la longitud de la señal.
3. Teorema de convolución
El teorema de convolución explica la relación importante entre la operación de convolución y la transformada de Fourier. Su núcleo es que la convolución en el dominio temporal se transforma en una simple multiplicación en el dominio de frecuencia.
Teorema de convolución: La transformada de Fourier de la convolución \(f(t) * g(t)\) de dos funciones \(f(t)\) y \(g(t)\) es igual al producto de las transformadas de Fourier de cada función.
\(\mathcal{F}\{f * g\} = \mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\)
Es decir, si \(F(\omega)\) y \(G(\omega)\) son las transformadas de Fourier de \(f(t)\) y \(g(t)\) respectivamente, entonces la transformada de Fourier de \(f(t) * g(t)\) es \(F(\omega)G(\omega)\).
Interpretación en el dominio de la frecuencia: El teorema de convolución permite interpretar la operación de convolución en el dominio de la frecuencia. Los filtros de convolución desempeñan un papel en enfatizar o suprimir componentes de frecuencia específicas de la señal de entrada. La multiplicación en el dominio de la frecuencia es equivalente a ajustar la amplitud de los componentes de frecuencia correspondientes.
4. Respuesta en frecuencia del filtro de convolución (Frequency Response)
Al analizar la respuesta en frecuencia de diferentes filtros de convolución, podemos determinar qué componentes de frecuencia pasan y cuáles son bloqueadas por el filtro.
Visualización de la respuesta en frecuencia: Se puede obtener la respuesta en frecuencia calculando la transformada de Fourier del filtro. La respuesta en frecuencia generalmente se expresa en términos de magnitud (magnitude) y fase (phase). La magnitud muestra los cambios de amplitud en cada componente de frecuencia, mientras que la fase representa los cambios de fase.
Tipos de filtros:
- Low-pass filter (filtro de paso bajo): Permite pasar componentes de baja frecuencia y bloquea las de alta frecuencia. Tiene el efecto de suavizar (blurring) imágenes (por ejemplo, filtro Gaussiano).
- High-pass filter (filtro de paso alto): Permite pasar componentes de alta frecuencia y bloquea las de baja frecuencia. Tiene el efecto de resaltar los bordes (edge) en las imágenes (por ejemplo, filtro Sobel).
- Band-pass filter (filtro de paso de banda): Permite pasar solo un rango específico de frecuencias y bloquea el resto.
A continuación se muestra un ejemplo de la visualización de la respuesta en frecuencia del filtro Sobel y del filtro Gaussiano. (Ejecutar el código generará una imagen.)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d
def plot_frequency_response(kernel, title):
# Calculate the 2D FFT of the kernel
kernel_fft = np.fft.fft2(kernel, s=(256, 256)) # Zero-padding for better visualization
kernel_fft_shifted = np.fft.fftshift(kernel_fft) # Shift zero frequency to center
# Calculate the magnitude and phase
magnitude = np.abs(kernel_fft_shifted)
phase = np.angle(kernel_fft_shifted)
# Plot the magnitude response
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(np.log(1 + magnitude), cmap='gray') # Log scale for better visualization
plt.title(f'{title} - Respuesta de Magnitud')
plt.colorbar()
plt.axis('off')
#Plot the phase response
plt.subplot(1, 2, 2)
plt.imshow(phase, cmap='hsv')
plt.title(f'{title} - Respuesta de Fase')
plt.colorbar()
plt.axis('off')
plt.show()5. Interpretación en el dominio de la frecuencia de las convoluciones 1x1
1x1 convoluciones mantienen la información espacial intacta mientras realizan operaciones entre canales.
Combinación lineal entre canales: 1x1 convoluciones realizan una combinación lineal de los canales en cada posición de píxel. Esto se puede interpretar como un peso de la suma de las componentes de frecuencia de cada canal en el dominio de la frecuencia. Es decir, los pesos del filtro de convolución 1x1 representan la importancia de las componentes de frecuencia de cada canal.
Ajuste de correlación y reconstrucción de características: 1x1 convoluciones ajustan la correlación entre canales. Combinan canales con fuertes correlaciones o eliminan canales innecesarios para reconstruir la representación de las características.
Función en los módulos Inception: En los módulos Inception, 1x1 convoluciones desempeñan dos roles importantes.
- Reducción de dimensiones: Reducen el número de canales para disminuir la cantidad de cálculos.
- Añadir no linealidad: Se aplica una función de activación no lineal, como ReLU, después de 1x1 convoluciones para aumentar la capacidad de representación del modelo. Desde la perspectiva de respuesta en frecuencia, esto permite mezclar canales con diferentes respuestas en frecuencia y crear respuestas en frecuencia más complejas.
7.1.4 Cálculo de parámetros aprendibles de CNN
Calcular el número de parámetros aprendibles en una CNN es muy importante para el diseño y la optimización de la red. Veamos esto paso a paso.
1. Capa de convolución básica
conv = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3)El cálculo de parámetros es el siguiente: - Tamaño de cada filtro: 3 × 3 × 1 (tamaño del kernel² × canales de entrada) - Número de filtros: 32 (canales de salida) - Sesgo (bias): 32 (igual al número de canales de salida) - Parámetros totales = (3 × 3 × 1) × 32 + 32 = 320
2. Capa de max pooling
maxpool = nn.MaxPool2d(kernel_size=2, stride=2)- No hay parámetros aprendibles
- Solo realiza la operación de seleccionar el valor máximo en una región de 2×2
- Reduce el tamaño del mapa de características (la altura y ancho se reducen a 1/2)
3. Convolución con padding
conv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1)El padding solo afecta el tamaño de salida y no cambia el número de parámetros. - Tamaño de cada filtro: 3 × 3 × 3 - Número de filtros: 64 - Parámetros totales = (3 × 3 × 3) × 64 + 64 = 1,792
4. Combinación de convolución con stride y pooling
conv = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=2)
maxpool = nn.MaxPool2d(kernel_size=2, stride=2)- Parámetros de convolución = (3 × 3 × 64) × 128 + 128 = 73,856
- Parámetros de pooling = 0
- Parámetros totales = 73,856
Cálculo del tamaño de salida.
Tamaño de salida de convolución = ((tamaño de entrada + 2×padding - tamaño del kernel) / stride) + 1
Tamaño de salida de pooling = ((tamaño de entrada - tamaño de pooling) / stride de pooling) + 15. Ejemplo de estructura compleja (bloque básico de ResNet)
Code
class BasicBlock(nn.Module):
def __init__(self, in_channels=64, out_channels=64):
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)
self.bn1 = nn.BatchNorm2d(out_channels)
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
self.bn2 = nn.BatchNorm2d(out_channels)
self.maxpool = nn.MaxPool2d(kernel_size=2, stride=2)Cálculo de parámetros. 1. Primera convolución: (3 × 3 × 64) × 64 + 64 = 36,928 2. Primera normalización por lotes: 64 × 2 = 128 (gamma y beta) 3. Segunda convolución: (3 × 3 × 64) × 64 + 64 = 36,928 4. Segunda normalización por lotes: 64 × 2 = 128 5. Max pooling: 0
Parámetros totales = 74,112
Este cálculo del número de parámetros es crucial para comprender la complejidad del modelo, predecir los requisitos de memoria y evaluar el riesgo de sobreajuste. En particular, las capas de pooling reducen eficazmente el tamaño de los mapas de características sin parámetros, lo que ayuda significativamente a aumentar la eficiencia computacional.
7.1.5 CNN: Aprendizaje de extracción y abstracción de características
El núcleo del CNN es extraer las características de una imagen a través de “filtros aprendibles” y combinarlas jerárquicamente para aprender representaciones más abstractas. Este proceso comienza con los detalles específicos de la imagen, avanzando hasta comprender el significado abstracto (por ejemplo, el tipo de objeto) y puede dividirse en dos aspectos principales.
- Extracción y transformación de características de imagen (Feature Extraction and Transformation): se extraen las características del área local de una imagen y solo se conservan las características significativas a través de funciones de activación no lineales.
- Aumento del número de filtros (canales) y expansión del espacio abstracto (Increasing Filters and Expanding Abstract Space): a medida que aumenta la profundidad, el número de filtros (canales) se incrementa para aprender características más diversas y abstractas.
1. Extracción y transformación de características de imagen
Las capas convolucionales del CNN aplican filtros aprendibles a la imagen de entrada (o a los mapas de características de la capa anterior) para extraer las características. Cada filtro se entrena para responder a patrones específicos en la imagen (por ejemplo, bordes, texturas, formas). Este proceso consta de los siguientes pasos.
- Operación convolucional: el filtro interactúa con el área local (campo receptivo) de la imagen y produce un valor que indica si existe un patrón específico en esa región. A través de este proceso, se genera un mapa de características (feature map) que representa la intensidad del patrón detectado por el filtro en cada ubicación de la imagen.
- Función de activación: el resultado de la operación convolucional (mapa de características) pasa a través de una función de activación no lineal, como ReLU. La función de activación transmite solo las características que superan un umbral específico a la siguiente capa y descarta las que no lo hacen. Esto ayuda a la red a centrarse en las características importantes y a eliminar la información innecesaria. (Representación dispersa)
- Pooling (opcional): la capa de pooling reduce el tamaño del mapa de características (downsampling) mientras fortalece la invariancia posicional (translation invariance). Por ejemplo, el max pooling conserva solo las características con los valores más altos en un área específica (por ejemplo, 2x2) y descarta el resto.
A través de este proceso, cada capa convolucional del CNN transforma la imagen de entrada a un espacio de características.
2. Aumento del número de filtros y expansión del espacio abstracto
El CNN tiene varias capas, y mientras se pasa por cada una, el tamaño espacial (ancho, alto) del mapa de características generalmente disminuye, mientras que el número de filtros (canales) aumenta. Este es el mecanismo clave a través del cual el CNN aprende abstracción.
- Reducción del tamaño espacial: la operación convolucional (stride > 1) o pooling reduce el tamaño espacial del mapa de características. Esto disminuye la cantidad de cálculos y fortalece la invariancia posicional, lo que permite reconocer un objeto incluso si se mueve ligeramente en la imagen.
- Aumento del número de canales: cada capa convolucional utiliza múltiples filtros para capturar aspectos diversos del mapa de características de entrada.
- Capas iniciales: detectan características de bajo nivel, como bordes y cambios de color. Estas características de bajo nivel representan los componentes básicos de la imagen.
- Capas intermedias: combinan las características de bajo nivel extraídas en las capas iniciales para detectar características de medio nivel como texturas, patrones y formas simples.
- Capas profundas: combinan las características extraídas en capas anteriores para detectar características de alto nivel y abstractas, como partes de un objeto (ojos, nariz, boca) e incluso el objeto completo (persona, automóvil, animal). El aumento en el número de filtros (canales) significa que la dimensión de las características que CNN utiliza para representar imágenes aumenta. Mientras que las capas iniciales se centran en los detalles concretos de la imagen, las capas profundas aprenden información necesaria para comprender el significado abstracto de la imagen. Esto es similar a cómo un humano ve los objetos, prestando atención inicialmente a los detalles específicos y gradualmente comprendiendo la forma general y el significado.
Ejemplo representativo de la estructura de capas CNN (VGGNet):
A continuación se muestra una figura que ilustra la arquitectura VGGNet. VGGNet es un modelo prototípico que ha estudiado sistemáticamente cómo afecta la profundidad de CNN al rendimiento.
- Arquitectura VGGNet:
Fuente: K. Simonyan, A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv:1409.1556, 2014.
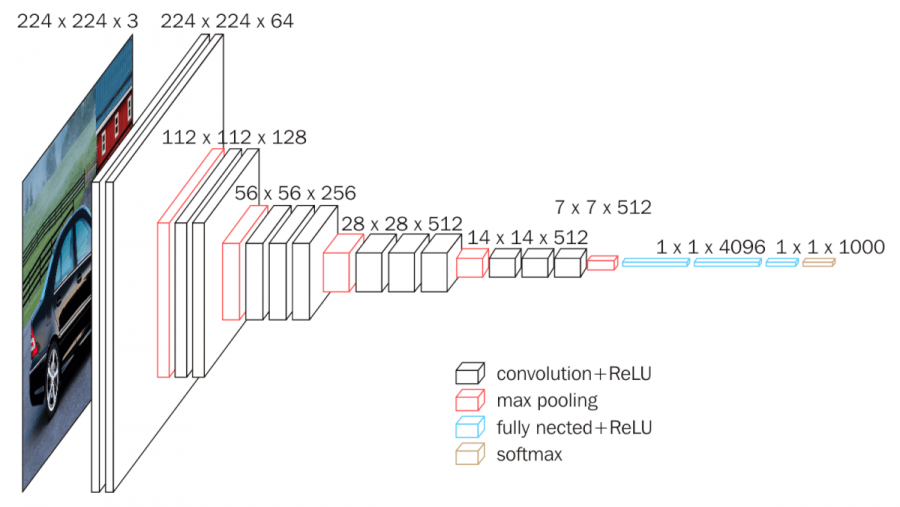
Como se puede ver en la figura, VGGNet tiene una estructura de múltiples capas convolucionales y de pooling apiladas. A medida que pasamos a través de cada capa, el tamaño espacial de los mapas de características disminuye, mientras que el número de canales aumenta. Esto visualiza cómo CNN transforma las imágenes desde una representación concreta de baja dimensión (valores de píxeles) a una representación abstracta de alta dimensión (tipo de objeto).
En conclusión, los “filtros aprendibles” de CNN son una herramienta poderosa para extraer características de imágenes y combinarlas jerárquicamente para aprender representaciones más abstractas. A través de múltiples capas de convolución y operaciones de pooling, CNN transforma las imágenes en representaciones más pequeñas, más profundas y más abstractas, aprendiendo información clave necesaria para comprender el significado de las imágenes desde los datos. Esta capacidad de extracción de características y abstracción es la razón principal por la que CNN tiene un rendimiento sobresaliente en diversas tareas de visión por computadora, como reconocimiento de imágenes, detección de objetos y segmentación de imágenes.
Haz clic para ver el contenido (análisis detallado: los diversos significados del término ‘kernel’ en deep learning y machine learning)
Significado diverso del término “kernel” en deep learning y machine learning
“Las palabras no tienen significado por sí mismas, sino en el contexto.” - (principio básico de la semántica/pragmática)
Al estudiar deep learning, machine learning y procesamiento de señales, nos encontramos con frecuencia con el término “kernel”. El “kernel” se usa con significados muy diferentes según el contexto, lo que puede causar confusión a los que lo ven por primera vez. En este análisis en profundidad, aclararemos los diversos contextos y significados de “kernel”, y examinaremos las relaciones entre sus usos.
1. Kernel (Kernel de Convolución) en redes neuronales convolucionales (CNN)
En CNN, el kernel se usa como sinónimo de filtro(filter). Es una pequeña matriz que realiza la operación de convolución sobre los datos de entrada (imágenes o mapas de características) en la capa de convolución.
Función: extrae características de regiones locales del imagen.
Forma de funcionamiento: el kernel se desplaza (stride) sobre los datos de entrada, multiplicando los valores de píxeles que se superponen con los pesos del kernel y sumando todos estos valores (operación de convolución). Este proceso genera un valor único que indica cuán fuertemente aparece el patrón que el kernel está diseñado para detectar (por ejemplo, bordes, texturas) en esa posición.
Aprendible: los pesos del kernel en una CNN se aprenden a partir de los datos mediante el algoritmo de retropropagación (backpropagation). Es decir, la CNN ajusta por sí misma los kernels para extraer las características más útiles para resolver un problema dado (por ejemplo, clasificación de imágenes).
Ejemplo: Kernel de Sobel
$
\[\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}\]$ Este kernel de Sobel de tamaño 3x3 se utiliza para detectar bordes verticales en imágenes.
Clave: En una CNN, el kernel tiene parámetros aprendibles y desempeña la función de extraer características locales de las imágenes.
2. Kernel (Función Kernel, Técnica del Kernel) en máquinas de vectores de soporte (SVM)
En SVM (Support Vector Machine), el kernel es una función que calcula la similitud entre dos puntos de datos. La SVM mapea los datos a un espacio de características de alta dimensión para resolver problemas de clasificación no lineal. La técnica del kernel permite calcular el producto interno en este espacio de alta dimensión implícitamente, sin necesidad de calcular explícitamente el mapeo.
- Función: mapea los datos a un espacio de características de alta dimensión para convertir problemas de clasificación no lineal en problemas de clasificación lineal.
- Clave: calcula eficientemente el producto interno en el espacio de características de alta dimensión (sin mapeo explícito).
- Expresión matemática: \(K(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x}) \cdot \phi(\mathbf{y})\)
- \(K(\mathbf{x}, \mathbf{y})\): función kernel (similitud entre los vectores de entrada \(\mathbf{x}\), \(\mathbf{y}\))
- \(\phi(\mathbf{x})\): función que mapea el vector de entrada \(\mathbf{x}\) al espacio de características de alta dimensión
- \(\cdot\): producto interno (inner product)
- Funciones de núcleo típicas:
- Núcleo lineal (Linear Kernel): \(K(\mathbf{x}, \mathbf{y}) = \mathbf{x}^T \mathbf{y}\) (producto interno simple)
- Núcleo polinomial (Polynomial Kernel): \(K(\mathbf{x}, \mathbf{y}) = (\gamma \mathbf{x}^T \mathbf{y} + r)^d\)
- Núcleo RBF (Radial Basis Function Kernel, Núcleo gaussiano): \(K(\mathbf{x}, \mathbf{y}) = \exp(-\gamma \|\mathbf{x} - \mathbf{y}\|^2)\) (más comúnmente utilizado)
- Núcleo sigmoide (Sigmoid Kernel): \(K(\mathbf{x}, \mathbf{y}) = \tanh(\gamma \mathbf{x}^T \mathbf{y} + r)\)
- Núcleos en SVM: El núcleo en SVM es una función que mide la similitud entre datos y permite resolver problemas no lineales mediante un mapeo implícito a un espacio de características de alta dimensión.
3. Núcleos en probabilidad y estadística (Kernel Density Estimation)
En probabilidad y estadística, el núcleo es una función no negativa que es simétrica alrededor del origen y cuyo valor integral es 1. Se utiliza en la estimación de densidad de kernel (KDE) para estimar la función de densidad de probabilidad a partir de datos dados (muestras). KDE es un método no paramétrico que estima la función de densidad de probabilidad basándose en los datos proporcionados.
- Función: Se utiliza como “función de peso” para estimar la densidad alrededor de los puntos de datos.
- Núcleos en KDE: Cada punto de datos se superpone con una función de núcleo para representar suavemente (smooth) la distribución general de los datos.
- Expresión matemática: \(\hat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right)\)
- \(\hat{f}(x)\): densidad de probabilidad estimada en \(x\)
- \(n\): número de puntos de datos
- \(h\): ancho de banda (bandwidth) - parámetro que ajusta el “ancho” del núcleo (parámetro de suavizado)
- \(K(\cdot)\): función de núcleo
- \(x_i\): punto de datos en la posición \(i\)
- Funciones de núcleo típicas:
- Núcleo gaussiano (Gaussian Kernel): \(K(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2}\) (más comúnmente utilizado)
- Núcleo Epanechnikov: \(K(x) = \frac{3}{4}(1 - x^2) \text{ si } |x| \le 1\)
- Núcleo uniforme (Box Kernel): \(K(x) = \frac{1}{2} \text{ si } |x| \le 1\)
- Función de los núcleos en KDE: Las funciones de núcleo en KDE actúan como “funciones de peso” para estimar la función de densidad de probabilidad.
4. Núcleo del sistema operativo (Operating System Kernel)
En ciencias de la computación, y especialmente en el campo de los sistemas operativos, el núcleo es un componente central del sistema operativo que actúa como interfaz entre el hardware y las aplicaciones, funcionando al nivel más bajo del sistema.
- Funciones:
- Gestión de procesos
- Gestión de memoria
- Gestión del sistema de archivos
- Gestión de entrada/salida (I/O)
- Gestión de recursos de hardware
- Ejemplos: Núcleo Linux, Núcleo Windows NT, Núcleo XNU de macOS
Resumen y comparación
| Campo | Significado del kernel | Papel principal |
|---|---|---|
| CNN | Filtro que realiza operaciones de convolución (matriz de pesos aprendibles) | Extracción de características locales de la imagen |
| SVM | Función que calcula la similitud entre dos puntos de datos (mapeo implícito a un espacio de características de alta dimensión) | Mapear datos no lineales a un espacio de alta dimensión para hacerlos separables linealmente |
| Probabilidad/Estadística (KDE) | Función de peso utilizada para estimar la función de densidad de probabilidad | Estimar suavemente la distribución de los datos |
| Sistema Operativo | Componente central del sistema operativo (interfaz entre el hardware y las aplicaciones) | Gestión de recursos del sistema, abstracción de hardware |
| Álgebra Lineal | Espacio nulo o núcleo de una transformación lineal (o matriz), es decir, el conjunto de vectores \(\mathbf{x}\) que satisfacen \(A\mathbf{x}=\mathbf{0}\) (para la transformación lineal \(T:V→W\) se tiene \(\text{Ker}(T)=\{\mathbf{v}∈V∣T(\mathbf{v})=\mathbf{0}\}\)) | Muestra las características de una transformación lineal |
En el caso del deep learning, especialmente en CNN, cuando se menciona “núcleo”, en la mayoría de los casos se refiere a un filtro de convolución. Sin embargo, es importante recordar que al encontrarse con otros algoritmos de machine learning como SVM o procesos gaussianos, el término puede referirse a una función núcleo. Es crucial comprender el significado exacto de “núcleo” según el contexto.
7.2 Aparición de ResNet
Desafío: ¿Cómo podemos aumentar efectivamente la profundidad de las redes neuronales sin sufrir problemas de desvanecimiento o explosión del gradiente, y al mismo tiempo asegurar un aprendizaje estable?
Lucha de los investigadores: A medida que las CNN mostraron un rendimiento excepcional en el reconocimiento de imágenes, los investigadores se esforzaron por crear redes más profundas. Sin embargo, a medida que la red se hacía más profunda, surgían problemas de desvanecimiento (vanishing gradients) y explosión (exploding gradients) del gradiente durante el proceso de retropropagación, lo cual impedía un aprendizaje efectivo. La repetición de transformaciones lineales simples limitaba la capacidad expresiva de las redes profundas. ¿Cómo podían superar estas limitaciones fundamentales y aprovechar al máximo la profundidad de las redes neuronales?
Con el éxito asombroso de las CNN en el campo del reconocimiento de imágenes, los investigadores naturalmente se preguntaron: “¿Podrían las redes más profundas ofrecer un mejor rendimiento?” Teóricamente, las redes más profundas deberían ser capaces de aprender características más complejas y abstractas. Sin embargo, en la práctica, a medida que la red se hacía más profunda, se observaba que el error de entrenamiento (training error) aumentaba.
7.2.1 Problemas con las redes neuronales profundas y el nacimiento de ResNet
En 2015, un equipo de investigación de Microsoft (Kaiming He et al.) presentó una solución innovadora a este problema en un artículo. Demostraron experimentalmente que la dificultad en el aprendizaje de las redes profundas no se debía a sobreajuste, sino a problemas de optimización que impedían reducir adecuadamente el error incluso en los datos de entrenamiento.
El equipo observó que una red neuronal de 56 capas presentaba un mayor error en los datos de entrenamiento comparado con una red de 20 capas. Este resultado contradecía la intuición de que una red de 56 capas debería ser al menos tan efectiva como una red de 20 capas (la red de 56 capas podría representar las funciones de la red de 20 capas si las restantes 36 capas aprendieran una mapeo de identidad, identity mapping). Esto planteó la pregunta fundamental: “¿Por qué las redes neuronales no pueden aprender incluso un simple mapeo de identidad a medida que se hacen más profundas?”
Para resolver este problema, el equipo propuso aprendizaje residual (Residual Learning), una idea muy simple pero poderosa. La clave era que en lugar de hacer que la red neuronal aprendiera directamente la función objetivo \(H(x)\), debía aprender la diferencia, es decir, el residuo (residual) \(F(x) = H(x) - x\) entre la entrada \(x\) y la función objetivo \(H(x)\).
\[ H(x) = F(x) + x \]
- \(x\): entrada
- \(F(x)\): función residual (residual function) - el objetivo de aprendizaje de la red neuronal
- \(H(x)\): función objetivo (desired mapping)
Si el mapeo de identidad (\(H(x) = x\)) es óptimo, la red neuronal solo tiene que aprender a hacer que la función residual \(F(x)\) sea 0. Esto es mucho más fácil que aprender toda la función \(H(x)\).
Conexión residual (Residual Connection / Skip Connection):
La implementación de la idea del aprendizaje residual se conoce como conexión residual (residual connection) o conexión de salto (skip connection). La conexión residual crea un camino que sume directamente la entrada \(x\) a la salida de la capa.
Comprensión intuitiva de ResNet:
Las conexiones residuales en ResNet son similares a los circuitos de realimentación (feedback) en ingeniería eléctrica. Aunque la señal de entrada puede distorsionarse o debilitarse al pasar por las capas, el camino directo de la señal original (conexión atajo, shortcut connection) permite que la información (y el gradiente) fluya a través de la red sin pérdida.
Éxito de ResNet: ResNet logró entrenar con éxito redes muy profundas, como la de 152 capas, que anteriormente eran imposibles de entrenar, a través del aprendizaje residual y las conexiones skip. Como resultado, ganó el desafío ILSVRC (ImageNet Large Scale Visual Recognition Challenge) de 2015 con una tasa de error asombrosa del 3.57%, inferior a la tasa de error humana (aproximadamente 5%).
Las conexiones residuales de ResNet son una idea simple pero muy poderosa, que tuvo un impacto significativo en el desarrollo posterior de arquitecturas de deep learning.
- Transformer (2017): La arquitectura Transformer, que revolucionó el procesamiento del lenguaje natural, adoptó las conexiones skip de ResNet en forma de capas “Add & Norm”.
- DenseNet (2017): DenseNet extendió la idea de ResNet para usar “conexiones densas”, donde cada capa está directamente conectada con las salidas de todas las capas anteriores.
- Inception-ResNet: Este modelo combina los módulos Inception de GoogLeNet con las conexiones residuales de ResNet.
- EfficientNet, MobileNetV2: Las redes ligeras como EfficientNet y MobileNetV2 también adoptaron el concepto de aprendizaje residual de ResNet.
7.2.2 Estructura y elementos clave de ResNet
ResNet se compone principalmente de dos tipos de bloques, es decir, el bloque básico (Basic Block) y el bloque de cuello de botella (Bottleneck Block).
- Bloque básico (Basic Block): Se utiliza en ResNet-18 y ResNet-34. Está formado por dos capas de convolución 3x3, y detrás de cada capa de convolución sigue una normalización por lotes (Batch Normalization) y la función de activación ReLU. Y lo más importante, la conexión residual (residual connection) se configura sumando la entrada de estas dos capas a la salida.
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicBlock(nn.Module):
"""Basic block for ResNet
Consists of two 3x3 convolutional layers
"""
expansion = 1 # Output channel expansion factor
def __init__(self, in_channels, out_channels, stride=1):
super().__init__()
# First convolutional layer
self.conv1 = nn.Conv2d(in_channels, out_channels,
kernel_size=3, stride=stride, padding=1)
self.bn1 = nn.BatchNorm2d(out_channels)
# Second convolutional layer
self.conv2 = nn.Conv2d(out_channels, out_channels * self.expansion,
kernel_size=3, stride=1, padding=1)
self.bn2 = nn.BatchNorm2d(out_channels * self.expansion)
# Skip connection (adjust dimensions with 1x1 convolution if necessary)
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels * self.expansion:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * self.expansion,
kernel_size=1, stride=stride),
nn.BatchNorm2d(out_channels * self.expansion)
)
def forward(self, x):
# Main path
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
# Add skip connection
out += self.shortcut(x)
out = F.relu(out)
return out- Conexión residual (Residual Connection):
out += self.shortcut(x)es la parte clave. Añade directamente la entrada a la salida. - Ajuste de dimensiones: Si el número de canales de entrada y salida son diferentes, o si el stride no es 1 causando que el tamaño del mapa de características cambie, se aplica una convolución de 1x1 a través de
self.shortcutpara ajustar el número de canales y el tamaño.
Bloque de cuello de botella (Bottleneck Block)
Se utiliza en ResNet-50 y superior. Se emplea para crear redes más profundas de manera eficiente. Está compuesto por una combinación de convoluciones 1x1, 3x3, 1x1, estructuradas de tal manera que reducen temporalmente el número de canales (como un cuello de botella) y luego lo aumentan nuevamente.
Code
class Bottleneck(nn.Module):
"""병목(Bottleneck) 구조 구현"""
expansion = 4 # 출력 채널을 4배로 확장하는 상수
def __init__(self, in_channels, out_channels, stride=1):
"""
Args:
in_channels: 입력 채널 수
out_channels: 중간 처리 채널 수 (최종 출력은 이것의 expansion배)
stride: 스트라이드 크기 (기본값: 1)
"""
super().__init__()
# 1단계: 1x1 컨볼루션으로 채널 수를 줄임 (차원 감소)
# 예: 256 -> 64 채널로 감소
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=1)
self.bn1 = nn.BatchNorm2d(out_channels)
# 2단계: 3x3 컨볼루션으로 특징 추출 (병목 구간)
# 감소된 채널 수로 연산 수행 (예: 64채널에서 처리)
self.conv2 = nn.Conv2d(out_channels, out_channels,
kernel_size=3, stride=stride, padding=1)
self.bn2 = nn.BatchNorm2d(out_channels)
# 3단계: 1x1 컨볼루션으로 채널 수를 다시 늘림 (차원 복원)
# 예: 64 -> 256 채널로 확장 (expansion=4인 경우)
self.conv3 = nn.Conv2d(out_channels,
out_channels * self.expansion, kernel_size=1)
self.bn3 = nn.BatchNorm2d(out_channels * self.expansion)La estructura de cuello de botella (Bottleneck) tiene, como su nombre lo sugiere, una forma en la que la dimensión del canal se estrecha y luego se ensancha nuevamente, similar al cuello de una botella. Por ejemplo, si suponemos un mapa de características con 256 canales de entrada:
- Reducción de la dimensión de 256→64 mediante una convolución 1x1
- Realización de la convolución 3x3 en los 64 canales reducidos
- Restauración de la dimensión a 64→256 mediante una última convolución 1x1
Esta estructura tiene las siguientes ventajas: - Reducción de cálculos: se realiza la convolución 3x3, que es la más costosa, en un número menor de canales - Reducción del número de parámetros: el número total de parámetros disminuye significativamente en comparación con el bloque básico - Mantenimiento de la capacidad expresiva: se conserva la habilidad de aprender diversas características durante el proceso de expansión dimensional
Gracias a esta eficiencia, los modelos más profundos que ResNet-50 han adoptado la estructura de cuello de botella en lugar del bloque básico.
Existen dos formas de conexión residual. Si el número de canales de entrada y salida es el mismo, se realiza una conexión directa; si son diferentes, se usa una convolución 1x1 para ajustar el número de canales. Esta idea fue inspirada por los módulos Inception de GoogLeNet (2014).
ResNet constituye una red profunda apilando varios de estos bloques básicos o bloques de cuello de botella.
ResNet tiene varias versiones según la profundidad de la red (ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152, etc.).
- ResNet-18, ResNet-34: utilizan bloques básicos (Basic Block).
- ResNet-50, ResNet-101, ResNet-152: utilizan bloques de cuello de botella (Bottleneck Block).
La estructura general de ResNet es la siguiente.
- Capa de convolución inicial: utiliza una convolución de 7x7 y un max pooling para reducir el tamaño de las imágenes de entrada.
- Varios etapas (Stage): cada etapa consta de múltiples bloques (bloque básico o bloque de cuello de botella). En el primer bloque de cada etapa, se establece el stride a 2 para reducir a la mitad el tamaño del mapa de características (downsampling).
- Pooling promedio (Average Pooling): elimina las dimensiones espaciales del mapa de características. (global average pooling)
- Capa completamente conectada (Fully Connected Layer): realiza la clasificación de clases.
Profundidad de la red y número de bloques:
La profundidad de ResNet se determina por el número de bloques en cada etapa. Por ejemplo, ResNet-18 utiliza 2 bloques básicos en cada etapa ([2, 2, 2, 2]). ResNet-50 utiliza [3, 4, 6, 3] bloques de cuello de botella en cada etapa.
- ResNet-18:
- convolución inicial de 7x7: 1 capa
- bloque básico (2 convoluciones de 3x3): 2 capas x (2 + 2 + 2 + 2) = 16 capas
- capa final completamente conectada: 1 capa
- total 1 + 16 + 1 = 18 capas
Code
# 총 층수 = 1 + (2 × 2 + 2 × 2 + 2 × 2 + 2 × 2) + 1 = 18
def ResNet18(num_classes=10):
return ResNet(BasicBlock, [2, 2, 2, 2], num_classes) # 기본 블록 사용- ResNet-50:
- Convolución inicial de 7x7: 1 capa
- Bloques de cuello de botella (3 convoluciones): 3 capas x (3 + 4 + 6 + 3) = 48 capas
- Capa completamente conectada final: 1 capa
- Total 1 + 48 + 1 = 50 capas
Code
# 병목 블록: 1x1 → 3x3 → 1x1 구조
# 총 층수 = 1 + (3 × 3 + 3 × 4 + 3 × 6 + 3 × 3) + 1 = 50
def ResNet50(num_classes=10):
return ResNet(Bottleneck, [3, 4, 6, 3], num_classes) # 병목 블록 사용Principios de diseño de ResNet:
- Cuatro etapas: En cada etapa, el tamaño del mapa de características se reduce a la mitad y el número de canales se duplica. Esto sigue la filosofía de diseño de VGGNet.
- Más bloques en etapas intermedias: Generalmente, se colocan más bloques en la etapa intermedia (etapa 3). Esto se basa en evidencia empírica de que las características a nivel medio son importantes para el reconocimiento de objetos.
- Estructura de cuello de botella (redes profundas): A medida que la red se hace más profunda, se utiliza una estructura de cuello de botella para mejorar la eficiencia computacional.
Gracias a estas innovaciones estructurales, ResNet pudo aprender eficientemente redes muy profundas, convirtiéndose en el estándar de las arquitecturas de deep learning modernas. La idea de ResNet influyó en numerosos modelos variados como Wide ResNet, ResNeXt y DenseNet.
7.2.4 Entrenamiento de ResNet y visualización de extracción de características
Un ejemplo de entrenar el modelo ResNet-18 con el conjunto de datos FashionMNIST se encuentra en chapter_07/train_resnet.py.
Code
from dldna.chapter_07.train_resnet import train_resnet18, save_model
model = train_resnet18(epochs=10)
# Save the model
save_model(model)Vamos a examinar cómo ResNet extrae las características de una imagen. Utilizaremos un modelo entrenado de ResNet-18 para visualizar cómo cambian los mapas de características a medida que pasan por cada capa.
Code
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from dldna.chapter_07.resnet import ResNet18
from dldna.chapter_07.train_resnet import get_trained_model_and_test_image
from torchvision import datasets, transforms
%matplotlib inline
def visualize_features(model, image):
"""각 층의 특징 맵을 시각화하는 함수"""
features = {}
# 특징 맵을 저장할 훅 등록
def get_features(name):
def hook(model, input, output):
features[name] = output.detach()
return hook
# 각 주요 층에 훅 등록
model.conv1.register_forward_hook(get_features('conv1'))
for idx, layer in enumerate(model.layer1):
layer.register_forward_hook(get_features(f'layer1_{idx}'))
for idx, layer in enumerate(model.layer2):
layer.register_forward_hook(get_features(f'layer2_{idx}'))
for idx, layer in enumerate(model.layer3):
layer.register_forward_hook(get_features(f'layer3_{idx}'))
for idx, layer in enumerate(model.layer4):
layer.register_forward_hook(get_features(f'layer4_{idx}'))
# 모델에 이미지 통과
with torch.no_grad():
_ = model(image.unsqueeze(0))
# 특징 맵 시각화
plt.figure(figsize=(20, 10))
for idx, (name, feature) in enumerate(features.items(), 1):
plt.subplot(3, 6, idx)
# 각 층의 첫 번째 채널만 시각화
plt.imshow(feature[0, 0].cpu(), cmap='viridis')
plt.title(f'Layer: {name}')
plt.axis('off')
plt.tight_layout()
plt.show()
return features
model, test_image, label, pred, classes = get_trained_model_and_test_image()
# 원본 이미지 시각화
plt.figure(figsize=(4, 4))
plt.imshow(test_image.squeeze(), cmap='gray')
plt.title(f'Class: {classes[label]}')
plt.axis('off')
plt.show()
print(f"이미지 shape: {test_image.shape}")
print(f"실제 클래스: {classes[label]} (레이블: {label})")
print(f"예측 클래스: {classes[pred]} (레이블: {pred})")
# # ResNet 모델에 이미지 통과시키고 특징 맵 시각화
# model = ResNet18(in_channels=1, num_classes=10)
# model.load_state_dict(torch.load('../../models/resnet18_fashion.pth'))
# model.eval()
features = visualize_features(model, test_image)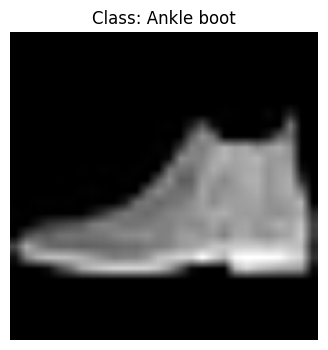
이미지 shape: torch.Size([1, 224, 224])
실제 클래스: Ankle boot (레이블: 9)
예측 클래스: Ankle boot (레이블: 9)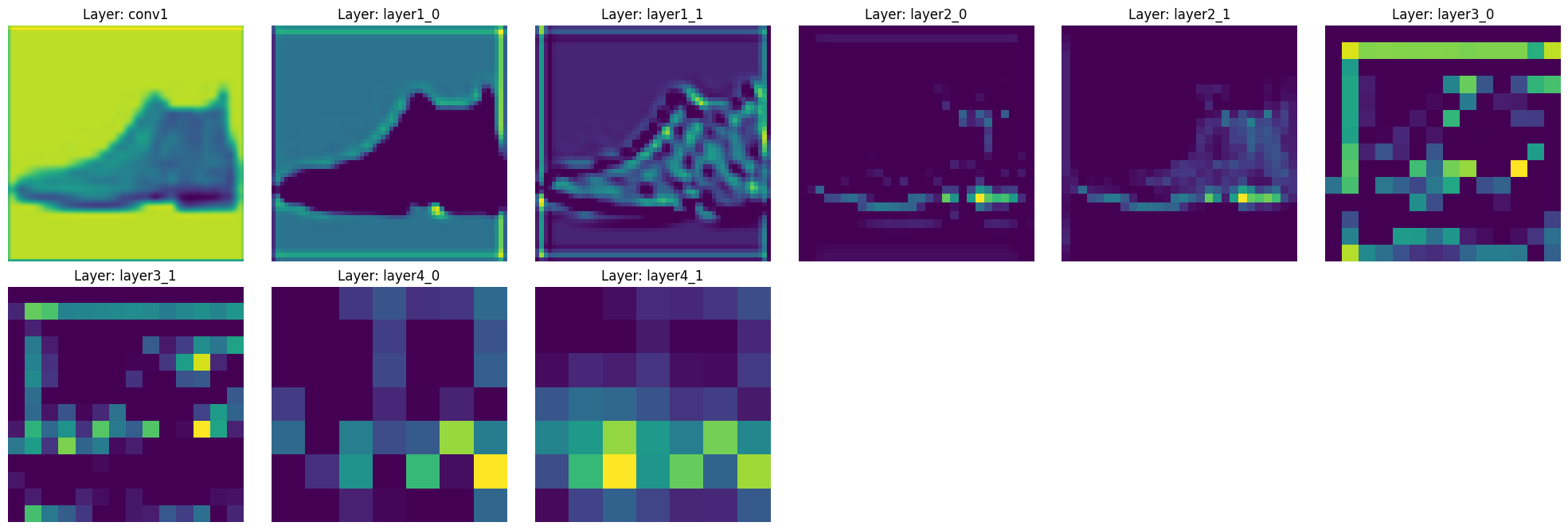
Al ejecutar este código, podemos ver cómo cambian las características a medida que pasan por las capas principales de ResNet-18.
- Convolución inicial (conv1) : extracción de información básica de forma, detección de características de nivel bajo como bordes y texturas.
- layer1 (bloque residual inicial) : combinación de características locales y comienzo de la composición de patrones simples.
- layer2 : aunque el tamaño del mapa de características disminuye, aumenta el número de canales, permitiendo reconocer patrones más complejos.
- layer3 : aumento en el nivel de abstracción, detección de características parciales de los objetos.
- layer4 (bloque residual final) : extracción de características abstractas y de alto nivel necesarias para distinguir las clases.
Esta extracción jerárquica de características es una de las principales fortalezas de ResNet. Gracias a las conexiones de salto, se puede observar que las características de cada capa se preservan bien mientras se abstraen gradualmente.
Haga clic para ver el contenido (deep dive: Módulo Inception - Agregando diversidad y eficiencia a las CNN)
Módulo Inception - Añadiendo diversidad y eficiencia a las CNN
El módulo Inception es un componente clave del GoogLeNet[^1], que ganó el ImageNet Large Scale Visual Recognition Challenge (ILSVRC) en 2014. Este módulo presentó una nueva aproximación a la estructura tradicional de las CNN, similar a su apodo “Network in Network”. Mientras que ResNet abordó el problema de la “profundidad”, el módulo Inception resolvió simultáneamente dos problemas importantes: “diversidad” y “eficiencia”. En este análisis en profundidad, examinamos las ideas clave, los principios matemáticos y el proceso evolutivo del módulo Inception, así como su impacto en el aprendizaje profundo, particularmente en el diseño de arquitecturas de CNN.
Idea clave del módulo Inception: Extracción de características “Multi-Escala”
El módulo Inception ofrece una solución elegante a este problema al utilizar filtros de diferentes tamaños en paralelo y combinar (concatenate) los resultados (mapas de características).
Idea clave:
- Filtros diversos: Aplica filtros de convolución de varios tamaños, como 1x1, 3x3, 5x5, a la misma entrada.
- Procesamiento en paralelo: Cada filtro realiza operaciones de convolución de manera independiente.
- Combinación (Concatenation): Combina los mapas de características generados por cada filtro a lo largo del eje de canales (channel).
- Conv1x1: Reduce el costo computacional, agrega no linealidad y mezcla la información entre canales. (“capa de cuello de botella”)
Módulo Inception v1 (GoogLeNet, 2014)
La primera versión del módulo Inception (GoogLeNet, [^1]) tiene la siguiente estructura.
- Entrada: Mapas de características (feature map) de la capa anterior.
- Ramas paralelas:
- Convolución 1x1
- Convolución 1x1 -> Convolución 3x3
- Convolución 1x1 -> Convolución 5x5
- Max pooling 3x3 -> Convolución 1x1
- Salida: Combina (concatenate) las salidas de cada rama a lo largo del eje de canales.
Rol de la convolución 1x1:
La convolución 1x1 desempeña un papel muy importante en el módulo Inception.
- Reducción dimensional (Dimensionality Reduction): Se utiliza para reducir el número de canales. Al usar una convolución 1x1 antes de las convoluciones 3x3 o 5x5, se puede reducir significativamente la cantidad de cálculos. (Capa de cuello de botella, Bottleneck Layer)
- Adición de no linealidad: Se puede agregar una función de activación como ReLU después de la convolución 1x1 para añadir no linealidad a la red.
- Mezcla de información entre canales: La convolución 1x1 calcula combinaciones lineales de los canales de entrada, lo que tiene el efecto de mezclar la información entre canales.
Limitaciones del módulo Inception v1:
- Las convoluciones 5x5 siguen siendo costosas en términos computacionales.
- La operación de pooling puede reducir la dimensión, pero también puede causar pérdida de información.
Módulo Inception v2 & v3 (2015)
Inception v2 y v3 introdujeron las siguientes ideas para superar las limitaciones de v1 [^2]. * Factorización: 5x5 convoluciones descompuestas en dos 3x3 convoluciones. (reducción de la cantidad de cálculos) * Convolución Asimétrica: 3x3 convolución descompuesta en una convolución 1x3 y una convolución 3x1. * Clasificador Auxiliar: se agrega un clasificador auxiliar durante el entrenamiento para mitigar el problema de la desaparición del gradiente y acelerar el aprendizaje. (eliminado en v3) * Label Smoothing: se añade ruido a las etiquetas correctas para prevenir que el modelo sea demasiado confiado (overconfidence).
Módulo Inception v4 (2016)
Inception-v4 introduce módulos de Inception-ResNet, combinando módulos de Inception con conexiones residuales de ResNet [^3].
Xception (2017)
Xception (“Extreme Inception”) es un modelo que lleva las ideas del módulo de Inception al extremo[^4]. Utiliza Convolución Profundizable (Depthwise Separable Convolution) para separar la convolución espacial por canal (depthwise convolution) y la convolución entre canales (pointwise convolution, 1x1 conv).
Expresión Matemática (Inception v1)
Cada rama del módulo de Inception se puede expresar como sigue.
- Rama 1: \(\text{Output}_1 = \text{Conv}_{1x1}(\text{Input})\)
- Rama 2: \(\text{Output}_2 = \text{Conv}_{3x3}(\text{Conv}_{1x1}(\text{Input}))\)
- Rama 3: \(\text{Output}_3 = \text{Conv}_{5x5}(\text{Conv}_{1x1}(\text{Input}))\)
- Rama 4: \(\text{Output}_4 = \text{Conv}_{1x1}(\text{MaxPool}(\text{Input}))\)
- Salida: \(\text{Concatenate}(\text{Output}_1, \text{Output}_2, \text{Output}_3, \text{Output}_4)\)
Aquí, \(\text{Conv}_{NxN}\) representa una operación de convolución de tamaño \(N \times N\), y \(\text{MaxPool}\) representa una operación de pooling máximo.
Similitud con la Transformada Wavelet
El enfoque multi-escala del módulo Inception es similar a la transformada wavelet (wavelet transform). La transformada wavelet descompone una señal en componentes de frecuencia variados. Cada filtro del módulo Inception (1x1, 3x3, 5x5) puede interpretarse como extrayendo características de bandas de frecuencia diferentes, es decir, de escalas diferentes. La convolución 1x1 extrae componentes de alta frecuencia, la 3x3 extrae componentes de frecuencia media, y la 5x5 extrae componentes de baja frecuencia.
Ventajas del Módulo Inception
- Extracción de Características Multi-Escala: al usar varios tamaños de filtros simultáneamente, captura eficazmente características de diversas escalas en una imagen.
- Eficiencia Computacional: reduce la cantidad de cálculos manteniendo la capacidad expresiva mediante el uso de convoluciones 1x1 para reducir las dimensiones.
- Rendimiento Potente: logra un nivel superior de rendimiento en el conjunto de datos ImageNet.
Impacto en el Ecosistema de Aprendizaje Profundo
El módulo Inception presentó una nueva perspectiva en el diseño de arquitecturas CNN. Demostró que no solo es importante ir “más profundo (deeper)”, sino también “más ancho (wider)” y “más diverso (more diverse)”. La idea del módulo Inception influyó posteriormente en el desarrollo de modelos ligeros como MobileNet, ShuffleNet, entre otros.
Implementación simple de un módulo Inception (PyTorch)
import torch
import torch.nn as nn
import torch.nn.functional as F
class InceptionModule(nn.Module):
def __init__(self, in_channels, out_channels_1x1, out_channels_3x3_reduce,
out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5,
out_channels_pool):
super().__init__()
# Rama de convolución 1x1
self.branch1x1 = nn.Conv2d(in_channels, out_channels_1x1, kernel_size=1)
# Rama de convolución 1x1 -> 3x3
self.branch3x3_reduce = nn.Conv2d(in_channels, out_channels_3x3_reduce, kernel_size=1)
self.branch3x3 = nn.Conv2d(out_channels_3x3_reduce, out_channels_3x3, kernel_size=3, padding=1)
# Rama de convolución 1x1 -> 5x5
self.branch5x5_reduce = nn.Conv2d(in_channels, out_channels_5x5_reduce, kernel_size=1)
self.branch5x5 = nn.Conv2d(out_channels_5x5_reduce, out_channels_5x5, kernel_size=5, padding=2)
# Rama de max pooling 3x3 -> convolución 1x1
self.branch_pool = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.branch_pool_proj = nn.Conv2d(in_channels, out_channels_pool, kernel_size=1)
def forward(self, x):
branch1x1 = F.relu(self.branch1x1(x))
branch3x3 = F.relu(self.branch3x3_reduce(x))
branch3x3 = F.relu(self.branch3x3(branch3x3))
branch5x5 = F.relu(self.branch5x5_reduce(x))
branch5x5 = F.relu(self.branch5x5(branch5x5))
branch_pool = F.relu(self.branch_pool_proj(self.branch_pool(x)))
outputs = [branch1x1, branch3x3, branch5x5, branch_pool]
return torch.cat(outputs, 1) # Concatenate along the channel dimensionEjemplo de uso
in_channels = 3 # Ejemplo de canales de entrada out_channels_1x1 = 64 out_channels_3x3_reduce = 96 out_channels_3x3 = 128 out_channels_5x5_reduce = 16 out_channels_5x5 = 32 out_channels_pool = 32
inception_module = InceptionModule(in_channels, out_channels_1x1, out_channels_3x3_reduce, out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5, out_channels_pool)
Ejemplo de tensor de entrada (tamaño_lote, canales, altura, anchura)
input_tensor = torch.randn(1, in_channels, 28, 28) output_tensor = inception_module(input_tensor) print(output_tensor.shape) # Verificar forma de salida
Este código implementa la estructura básica del Módulo Inception (v1) en PyTorch. En las bibliotecas `torchvision.models` o `timm`, se encuentran implementadas versiones más avanzadas de la red Inception (Inception-v3, Inception-v4, Inception-ResNet, etc.), por lo que es recomendable utilizar estas bibliotecas en proyectos reales.
---
[1]: Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., ... & Rabinovich, A. (2015). Going deeper with convolutions. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1-9).
[2]: Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., & Wojna, Z. (2016). Rethinking the inception architecture for computer vision. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 2818-2826).
[3]: Szegedy, C., Ioffe, S., Vanhoucke, V., & Alemi, A. A. (2017). Inception-v4, inception-resnet and the impact of residual connections on learning. In *Thirty-first AAAI conference on artificial intelligence*.
[4]: Chollet, F. (2017). Xception: Deep learning with depthwise separable convolutions. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1251-1258).7.3 EfficientNet: Escalado eficiente del modelo
Desafío: ¿Cómo se puede maximizar el rendimiento del modelo mientras se minimiza el costo computacional (número de parámetros, FLOPS)?
Lucha del investigador: La aparición de ResNet hizo posible entrenar redes profundas, pero no existía un método sistemático para ajustar el tamaño del modelo. Simplemente agregar capas o aumentar el número de canales puede aumentar significativamente el costo computacional. Los investigadores buscaron encontrar el equilibrio óptimo entre la profundidad (depth), anchura (width) y resolución (resolution) del modelo, para lograr el mejor rendimiento con los recursos computacionales disponibles.
7.3.1 Escalado compuesto: equilibrio de profundidad, anchura y resolución
La idea central de EfficientNet es el “Escalado Compuesto”. Mientras que investigaciones anteriores tendían a ajustar solo uno de los tres factores (profundidad, anchura, resolución), EfficientNet descubrió que es más eficiente ajustar estos tres factores simultáneamente y de manera equilibrada.
- Profundidad (Depth): Número de capas en la red. Las redes más profundas pueden aprender características más complejas, pero son propensas a problemas de desvanecimiento o explosión del gradiente y a overfitting.
- Anchura (Width): Número de canales (filtros) por capa. Las redes más anchas pueden aprender características más detalladas (fine-grained features), pero aumentan el costo computacional, el número de parámetros y el riesgo de overfitting.
- Resolución (Resolution): Tamaño de las imágenes de entrada. Las imágenes con mayor resolución contienen más información, pero aumentan significativamente el costo computacional.
EfficientNet demostró experimentalmente que estos tres factores están interrelacionados y que ajustarlos de manera equilibrada juntos es más efectivo que cambiar solo uno de ellos. Por ejemplo, si se duplica la resolución de las imágenes, debe aumentarse adecuadamente la profundidad y la anchura de la red para permitirle aprender patrones más finos. Simplemente aumentar la resolución puede resultar en una mejora mínima del rendimiento o incluso un empeoramiento.
En el artículo de EfficientNet, se define el problema de escalado del modelo como un problema de optimización y se expresa la relación entre profundidad (depth), anchura (width) y resolución (resolution) con las siguientes fórmulas.
Primero, si denotamos un modelo CNN por \(\mathcal{N}\), entonces la \(i\)-ésima capa puede representarse como una transformación funcional \(Y_i = \mathcal{F}_i(X_i)\). Aquí, \(Y_i\) es el tensor de salida, \(X_i\) es el tensor de entrada y \(\mathcal{F}_i\) es la operación. La forma del tensor de entrada \(X_i\) se puede representar como \(<H_i, W_i, C_i>\), donde cada uno representa altura (height), anchura (width) y número de canales (channel).
El modelo CNN completo \(\mathcal{N}\) puede representarse como la composición de las funciones de capa
\(\mathcal{N} = \mathcal{F}_k \circ \mathcal{F}_{k-1} \circ ... \circ \mathcal{F}_1 = \bigodot_{i=1...k} \mathcal{F}_i\)
En el diseño típico de un CNN, se centra en encontrar la operación de capa óptima \(\mathcal{F}_i\), pero EfficientNet se enfoca en ajustar la longitud (\(\hat{L}_i\)), anchura (\(\hat{C}_i\)) y resolución (\(\hat{H}_i, \hat{W}_i\)) de la red mientras mantiene fijas las operaciones de capa. Para esto, se define una red base (baseline network) como \(\hat{\mathcal{N}}\) y se expande el modelo multiplicándola por un coeficiente de escalado. Red de referencia: \(\hat{\mathcal{N}} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{L_i}(X_{<H_i, W_i, C_i>})\)
EfficientNet busca resolver el siguiente problema de optimización.
\(\underset{\mathcal{N}}{maximize}\quad Accuracy(\mathcal{N})\)
\(subject\ to\quad \mathcal{N} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{d \cdot \hat{L}_i}(X_{<r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i>})\)
\(Memory(\mathcal{N}) \leq target\_memory\)
\(FLOPS(\mathcal{N}) \leq target\_flops\)
Aquí, \(d\), \(w\), \(r\) son los coeficientes de escala para la profundidad, anchura y resolución, respectivamente.
EfficientNet propone un método de escalado compuesto (compound scaling) para simplificar este problema complejo de optimización, que busca maximizar la precisión mientras satisface todas las restricciones de recursos. El escalado compuesto usa un solo coeficiente (\(\phi\), coeficiente compuesto) para ajustar uniformemente la profundidad, anchura y resolución.
\(\begin{aligned} & \text{profundidad: } d = \alpha^{\phi} \\ & \text{anchura: } w = \beta^{\phi} \\ & \text{resolución: } r = \gamma^{\phi} \\ & \text{subject to } \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\ & \alpha \geq 1, \beta \geq 1, \gamma \geq 1 \end{aligned}\)
- \(\phi\) (phi) es un coeficiente (coeficiente compuesto) especificado por el usuario que controla el tamaño general del modelo.
- \(\alpha\), \(\beta\), \(\gamma\) son constantes que determinan cuánto se incrementará la profundidad, anchura y resolución, respectivamente. Estos valores se determinan mediante una búsqueda en una cuadrícula pequeña (small grid search). (\(\alpha\), \(\beta\), \(\gamma\) se encuentran fijando \(\phi=1\) y realizando una búsqueda pequeña.)
- La restricción (\(α ⋅ β² ⋅ γ² ≈ 2\)) asegura que los FLOPS del modelo aumenten aproximadamente en un factor de 2 cada vez que \(ϕ\) se incrementa en 1. Esta restricción se establece porque los FLOPS aumentan linealmente con la profundidad, y cuadráticamente con la anchura y resolución.
Usando este método de escalado compuesto, el usuario puede ajustar fácilmente el tamaño del modelo simplemente cambiando el valor de \(ϕ\), permitiendo un control efectivo del equilibrio entre el rendimiento y la eficiencia del modelo.
7.3.2 Arquitectura EfficientNet
EfficientNet utiliza la tecnología AutoML (Neural Architecture Search, NAS) para encontrar el mejor modelo base (baseline model), EfficientNet-B0, y luego aplica el escalado compuesto para generar modelos de diferentes tamaños (B1 a B7, e incluso L2 más grande).
Estructura de EfficientNet-B0:
EfficientNet-B0 se basa en bloques MBConv (Mobile Inverted Bottleneck Convolution), inspirados en MobileNetV2. Los bloques MBConv tienen la siguiente estructura para mejorar la eficiencia computacional. 1. Expansion (1x1 Conv): expande el número de canales de entrada (factor de expansión, típicamente 6). Al aumentar el número de canales usando una convolución 1x1, se puede reducir relativamente el costo computacional de las operaciones posteriores (convolución depthwise) mientras se mejora la expresividad.
Depthwise Separable Convolution:
- Depthwise Convolution (3x3): realiza una convolución espacial independiente en cada canal de entrada. A diferencia de las convoluciones estándar, no hay mezcla de información entre canales.
- Pointwise Convolution (1x1 Conv): usa una convolución 1x1 para mezclar la información entre canales.
La convolución depthwise separable puede reducir significativamente el número de parámetros y la cantidad de cálculos en comparación con las convoluciones estándar.
Squeeze-and-Excitation (SE) Block: aprende la importancia relativa entre los canales, enfatizando los canales más importantes. El bloque SE resume la información de cada canal usando un pooling promedio global y calcula pesos por canal utilizando dos capas fully connected.
Projection (1x1 Conv): reduce nuevamente el número de canales a su valor original (para las conexiones residuales).
Residual Connection: suma la entrada y la salida (cuando el número de canales de entrada es igual al número de canales de salida, y stride=1). Es una idea central en ResNet.
A continuación se muestra un ejemplo de implementación del bloque MBConv de EfficientNet-B0 usando PyTorch. (Se omite la implementación completa de EfficientNet-B0; puede importarse desde las bibliotecas torchvision o timm.)
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class MBConvBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride, expand_ratio=6, se_ratio=0.25, kernel_size=3):
super().__init__()
self.stride = stride
self.use_residual = (in_channels == out_channels) and (stride == 1) # 잔차 연결 조건
expanded_channels = in_channels * expand_ratio
# Expansion (1x1 conv)
self.expand_conv = nn.Conv2d(in_channels, expanded_channels, kernel_size=1, bias=False)
self.bn0 = nn.BatchNorm2d(expanded_channels)
# Depthwise convolution
self.depthwise_conv = nn.Conv2d(expanded_channels, expanded_channels, kernel_size=kernel_size,
stride=stride, padding=kernel_size//2, groups=expanded_channels, bias=False)
# groups=expanded_channels: depthwise conv
self.bn1 = nn.BatchNorm2d(expanded_channels)
# Squeeze-and-Excitation
num_reduced_channels = max(1, int(in_channels * se_ratio)) # 최소 1개는 유지
self.se_reduce = nn.Conv2d(expanded_channels, num_reduced_channels, kernel_size=1)
self.se_expand = nn.Conv2d(num_reduced_channels, expanded_channels, kernel_size=1)
# Pointwise convolution (projection)
self.project_conv = nn.Conv2d(expanded_channels, out_channels, kernel_size=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channels)
def forward(self, x):
identity = x
# Expansion
out = F.relu6(self.bn0(self.expand_conv(x)))
# Depthwise separable convolution
out = F.relu6(self.bn1(self.depthwise_conv(out)))
# Squeeze-and-Excitation
se = out.mean((2, 3), keepdim=True) # Global Average Pooling
se = F.relu6(self.se_reduce(se))
se = torch.sigmoid(self.se_expand(se))
out = out * se # 채널별 가중치 곱
# Projection
out = self.bn2(self.project_conv(out))
# Residual connection
if self.use_residual:
out = out + identity
return out
# Example usage
# in_channels = 32
# out_channels = 16
# stride = 1
# mbconv_block = MBConvBlock(in_channels, out_channels, stride)
# input_tensor = torch.randn(1, in_channels, 224, 224) # Example input
# output_tensor = mbconv_block(input_tensor)
# print(output_tensor.shape)7.3.3 Rendimiento e impacto de EfficientNet
EfficientNet logró una mayor precisión con significativamente menos parámetros y cálculos en comparación con los modelos CNN existentes (ResNet, DenseNet, Inception, etc.) en la clasificación de ImageNet. La siguiente tabla compara el rendimiento de EfficientNet con otros modelos.
| Modelo | Precisión Top-1 | Precisión Top-5 | Parámetros | FLOPS |
|---|---|---|---|---|
| ResNet-50 | 76.0% | 93.0% | 25.6M | 4.1B |
| DenseNet-169 | 76.2% | 93.2% | 14.3M | 3.4B |
| Inception-v3 | 77.9% | 93.8% | 23.9M | 5.7B |
| EfficientNet-B0 | 77.1% | 93.3% | 5.3M | 0.39B |
| EfficientNet-B1 | 79.1% | 94.4% | 7.8M | 0.70B |
| EfficientNet-B4 | 82.9% | 96.4% | 19.3M | 4.2B |
| EfficientNet-B7 | 84.3% | 97.0% | 66M | 37B |
| EfficientNet-L2* | 85.5% | 97.7% | 480M | 470B |
* Entrenamiento con Noisy Student
Como se puede ver en la tabla, EfficientNet-B0 logró una mayor precisión con menos parámetros y FLOPS que ResNet-50. EfficientNet-B7 alcanzó una precisión Top-1 del 84.3% (estado del arte en ese momento) en ImageNet, pero sigue siendo mucho más eficiente que otros modelos grandes.
Principales contribuciones de EfficientNet:
- Escalado compuesto: Propuso un nuevo método para ajustar equilibradamente la profundidad, el ancho y la resolución del modelo, mejorando la comprensión de la relación entre el tamaño del modelo y su rendimiento.
- Diseño eficiente del modelo: EfficientNet-B0, encontrado mediante AutoML (NAS), demostró ser más eficiente y potente que otros modelos diseñados manualmente.
- Práctico: EfficientNet ofrece una variedad de tamaños de modelos (B0 ~ B7, L2) para que los usuarios puedan elegir el modelo que se adapte a sus recursos de computación y requisitos de rendimiento.
Impacto en la academia y la industria:
EfficientNet ha fomentado investigaciones sobre la ligereza y eficiencia del modelo, y se utiliza ampliamente para implementar modelos de aprendizaje profundo en dispositivos móviles, sistemas embebidos y otros entornos con recursos limitados. La idea de escalado compuesto de EfficientNet también se ha aplicado a otros modelos, lo que ha llevado a mejoras en el rendimiento. Después de EfficientNet, se han realizado investigaciones posteriores enfocadas en la eficiencia como EfficientNetV2, MobileNetV3, RegNet, entre otras.
Limitaciones:
- Aún falta una explicación teórica completa sobre por qué la arquitectura de EfficientNet-B0 encontrada mediante AutoML (NAS) es más efectiva que otras arquitecturas.
- No se puede garantizar que el método de escalado compuesto sea óptimo para todos los tipos de arquitecturas de CNN y tareas. A pesar de ello, EfficientNet se considera un hito importante en la historia del aprendizaje profundo por presentar una nueva perspectiva en el diseño de modelos CNN y mejorar significativamente la eficiencia del modelo.
Conclusión
En este capítulo hemos examinado el contexto de surgimiento y desarrollo de las redes neuronales convolucionales (CNN), así como sus avances más importantes representados por ResNet, los módulos Inception y EfficientNet.
La CNN mostró grandes logros en el reconocimiento de imágenes a través de LeNet-5 y AlexNet, pero se enfrentó a dificultades con la profundización de las redes. ResNet resolvió este problema mediante conexiones residuales, permitiendo una expansión de profundidad revolucionaria. Los módulos Inception aumentaron la diversidad y eficiencia en la extracción de características utilizando filtros de diferentes tamaños en paralelo, mientras que EfficientNet presentó un método sistemático para ajustar equilibradamente la profundidad, anchura y resolución del modelo.
Estas innovaciones han contribuido significativamente a que las CNN desempeñen un papel crucial no solo en el reconocimiento de imágenes sino también en diversas tareas de visión por computadora. Sin embargo, si bien las CNN son fuertes para capturar patrones locales espaciales, no son adecuadas para datos secuenciales, especialmente para el procesamiento del lenguaje natural, donde la secuencia y las dependencias a largo plazo son importantes.
En el siguiente capítulo examinaremos la arquitectura Transformer, que modela las relaciones entre elementos en una secuencia utilizando solo el mecanismo de Atención sin recurrir a operaciones de convolución o pooling. El Transformer ha logrado mejoras revolucionarias en el procesamiento del lenguaje natural y actualmente está expandiendo su influencia a campos diversos como la visión por computadora y el procesamiento del habla. Al igual que las conexiones residuales de ResNet superaron las limitaciones de profundidad de las CNN, el mecanismo de Atención de los Transformers ha abierto un nuevo horizonte para el procesamiento de datos secuenciales.
Ejercicios de práctica
Problemas básicos
- Explique el papel que juega la operación de convolución en el procesamiento de imágenes y proporcione un ejemplo específico como el filtro Sobel.
- Explique el rol y las ventajas de la capa de pooling en una CNN, y compare las diferencias entre el max pooling y el average pooling.
- Explique cómo la conexión residual, que es la idea clave de ResNet, ayuda en el aprendizaje de redes profundas, relacionándola con los problemas de desvanecimiento y explosión del gradiente.
- Explique las ideas principales detrás del módulo Inception, como “el uso de filtros de diferentes tamaños” y el papel de la convolución 1x1.
- Explique qué es el “compound scaling” en EfficientNet y compare sus ventajas con los métodos tradicionales de ajuste de tamaño del modelo (ajuste solo de profundidad, ancho o resolución).
Problemas aplicados
- Implemente un modelo CNN simple usando PyTorch y entrénelo y evalúelo utilizando el conjunto de datos MNIST (incluyendo carga de datos, definición del modelo, bucle de entrenamiento y evaluación).
- Cargue el modelo ResNet-18 desde
torchvision.models, realice transfer learning con el conjunto de datos CIFAR-10 y evalúe su rendimiento (preprocesamiento de datos, carga del modelo, ajuste fino, evaluación). - Use la función
show_filter_effectsproporcionada enexpertai_srcpara comparar visualmente los efectos de varios filtros (borrosidad, afilado, detección de bordes, etc.) sobre una imagen y explique las características de cada filtro. - Elimine las conexiones residuales del código dado de ResNet (
BasicBlock,Bottleneck), entrene con los mismos datos y evalúe el cambio en el rendimiento, analizando las razones detrás de estos cambios. - Implemente la operación de convolución 2D directamente basándose en la clase
SimpleConv2d(usando NumPy o las operaciones detensorde PyTorch, sin usartorch.nn.Conv2d).
Problemas avanzados
- Explique matemáticamente por qué ocurren los problemas de desvanecimiento y explosión del gradiente en CNNs profundas y cómo la conexión residual de ResNet, la normalización por lotes y la convolución 1x1 del módulo Inception ayudan a mitigar estos problemas.
- Lea los artículos de ResNet, Inception y EfficientNet y compare y analice las ideas principales de cada modelo (ventajas y desventajas de cada uno, relaciones entre ellos, impacto en la investigación posterior).
- Derive o explique detalladamente la fórmula de compound scaling de EfficientNet (o basándose en el artículo) y describa cómo determinar el tamaño óptimo del modelo bajo restricciones computacionales dadas.
- Explique la relación entre los procesos Gaussianos y el aprendizaje de kernels profundos (Deep Kernel Learning) y qué ventajas ofrece DKL en comparación con las CNNs y los GP tradicionales.
- Encuentre al menos un ejemplo de un artículo relacionado con CNNs publicado en los últimos 1-2 años que desarrolle ideas de ResNet, Inception o EfficientNet, resuma su contenido y presente su opinión (por ejemplo, ConvNeXt, NFNet).
Haga clic para ver el contenido (soluciones de ejercicios)
Soluciones a los ejercicios de práctica
Problemas básicos
- Función de la convolución y filtro Sobel:
- Función: La convolución extrae características mediante el cálculo del producto ponderado entre los valores de píxeles de una imagen y los valores de un filtro (kernel). El filtro se desplaza sobre la imagen, calculando en cada posición la suma ponderada de los valores de píxeles y del filtro.
- Filtro Sobel: Se utiliza para detectar bordes (contornos) en imágenes. Los filtros Sobel vertical/horizontal detectan cambios de brillo en las direcciones vertical/horizontal, respectivamente.
- Capa de pooling:
- Función/ventajas: Reduce el tamaño (dimensionalidad espacial) de los mapas de características para disminuir la cantidad de cálculos y aumentar la invariancia a traslaciones (translational invariance), lo que ayuda a prevenir el sobreajuste.
- Pooling máximo (Max Pooling): Selecciona el valor máximo dentro del área. Conserva las características más prominentes.
- Pooling promedio (Average Pooling): Calcula el valor promedio dentro del área. Es menos sensible al ruido.
- Conexiones residuales de ResNet:
- Conexión residual: Conexión “atajo” que suma directamente la entrada a la salida. \(H(x) = F(x) + x\)
- Mitigación del desvanecimiento/explosión del gradiente: Como el gradiente se transmite directamente a través de las conexiones residuales, se propaga bien incluso en redes profundas. Ayuda a que la red neuronal aprenda fácilmente una función de identidad (identity mapping, \(F(x) = 0\)).
- Módulo Inception:
- Filtros de diversos tamaños: Utiliza filtros de diferentes tamaños, como 1x1, 3x3, 5x5, en paralelo para capturar simultáneamente características de diversas escalas dentro de una imagen.
- Convolución 1x1: Reducción de dimensiones entre canales y adición de no linealidad. Aumenta la capacidad expresiva del modelo mientras reduce la cantidad de cálculos. (Actúa como capa “bottleneck”)
- Escala compuesta de EfficientNet:
- Escala compuesta: Método para aumentar de manera equilibrada la profundidad (depth), anchura (width) y resolución (resolution) de la red. Utiliza un solo coeficiente (compound coefficient) para ajustar simultáneamente los tres elementos.
- Ventajas: Mejora eficientemente el rendimiento del modelo en comparación con métodos tradicionales (que solo cambian un elemento). Permite ajustar el tamaño del modelo para alcanzar el mejor rendimiento bajo restricciones de recursos computacionales.
Problemas aplicados
Implementación y entrenamiento de CNN con MNIST: (código omitido) Utiliza PyTorch para combinar
nn.Conv2d,nn.ReLU,nn.MaxPool2d,nn.Lineary otros para construir un modelo de CNN, y usaDataLoaderpara cargar los datos de MNIST y entrenar/evaluar el modelo.Aprendizaje por transferencia con ResNet-18: (código omitido) Carga
resnet18desdetorchvision.models, reemplaza la última capa (fully connected layer) para adaptarla a CIFAR-100 y realiza fine-tuning en algunas capas.Análisis de
show_filter_effects: (código omitido) La funciónshow_filter_effectsaplica diversos filtros (Desenfoque Gaussiano, Afilado, Detección de bordes, Emboss, Sobel X) a una imagen dada y visualiza los resultados. Cada filtro enfatiza o modifica características específicas de la imagen (borrosidad, nitidez, detección de bordes, etc.).Eliminación de conexiones residuales en ResNet: (código omitido) Al eliminar las conexiones residuales, el aprendizaje en redes profundas se dificulta debido a problemas de desvanecimiento/explosión del gradiente, lo que tiende a reducir el rendimiento.
2D convolución implementada directamente: (código omitido) se realiza una multiplicación elemento por elemento y suma con el kernel en cada posición del tensor de entrada utilizando bucles for anidados. Usar técnicas como
im2colpara convertirlo a multiplicación de matrices es más eficiente.
Problemas avanzados
Degradación/explotación del gradiente:
- Causa: durante la retropropagación, el gradiente se multiplica repetidamente según la regla de la cadena, lo que puede hacer que el gradiente sea muy pequeño (degradación) o muy grande (explotación) a medida que avanza hacia capas más profundas. Si la derivada de la función de activación es menor que 1 (por ejemplo, sigmoid, tanh), es probable que ocurra la degradación; si es mayor que 1, es probable que ocurra la explotación.
- Conexiones residuales en ResNet: el gradiente se transmite directamente a través de las conexiones residuales, lo que mitiga el problema de degradación/explotación del gradiente.
- Normalización por lotes: normaliza las entradas de cada capa para mantener los inputs de la función de activación dentro de un rango adecuado, reduciendo así la degradación/explotación del gradiente.
- Convolución 1x1 en Inception: reduce el número de canales y minimiza el cálculo, mitigando indirectamente la degradación/explotación del gradiente (debido a la reducción de parámetros).
Comparación entre ResNet, Inception, EfficientNet: (comparación detallada omitida)
- ResNet: permite el aprendizaje de redes profundas mediante conexiones residuales.
- Inception: utiliza filtros de diferentes tamaños en paralelo para extraer características a diferentes escalas. Usa convoluciones 1x1 para aumentar la eficiencia computacional.
- EfficientNet: ajusta equilibradamente la profundidad, anchura y resolución del modelo mediante el escalamiento compuesto, mejorando tanto la eficiencia como el rendimiento.
Escalamiento compuesto en EfficientNet: (derivación de fórmulas/explicación detallada omitida) ajusta la profundidad (α^Φ), anchura (β^Φ), y resolución (γ^Φ) usando un coeficiente compuesto (Φ). α, β, γ son constantes encontradas mediante búsqueda en cuadrícula. Restricción: α ⋅ β² ⋅ γ² ≈ 2.
Procesos Gaussianos (GP) y DKL:
- GP: distribución de probabilidad sobre funciones. Define la covarianza entre los valores de las funciones usando una función kernel. Proporciona incertidumbre en las predicciones a través de inferencia bayesiana.
- DKL (Deep Kernel Learning): utiliza redes neuronales profundas para extraer características de los datos y usar estas características como entrada para la función kernel del GP. Combina el poder de aprendizaje de representaciones de deep learning con la capacidad de estimación de incertidumbre del GP.
- Ventajas: eficiencia en datos, estimación de incertidumbre, representación flexible de características.
- Desventajas: sigue existiendo la complejidad computacional del GP.
Artículos de CNN recientes: (ejemplos: ConvNeXt, NFNet, etc. resumen y opiniones omitidos)
Referencias
- Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex (Hubel & Wiesel, 1962): Estudio sobre la corteza visual del gato. Artículo que inspiró el concepto de campo receptivo en las CNN. (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1359523/)
- The Scientist and Engineer’s Guide to Digital Signal Processing (Steven W. Smith): Libro que explica los principios básicos del procesamiento de señales digitales. Ayuda a comprender la convolución, los filtros, etc. (http://www.dspguide.com/pdfbook.htm)
- Gradient-based learning applied to document recognition (LeCun et al., 1998): Reconocimiento de caracteres utilizando CNN. Introducción a LeNet-5. (http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf)
- Deep Residual Learning for Image Recognition (He et al., 2015): Artículo original de ResNet. (https://arxiv.org/pdf/1512.03385.pdf)
- Network in Network (Lin et al., 2013): Artículo que propone la idea de convoluciones 1x1. (https://arxiv.org/pdf/1312.4400.pdf)
- Very Deep Convolutional Networks for Large-Scale Image Recognition (Simonyan & Zisserman, 2014): Artículo de VGGNet. (https://arxiv.org/pdf/1409.1557.pdf)
- Dive into Deep Learning (Zhang et al., 2023): En el capítulo 9 “Convolutional Neural Networks” se explican los conceptos básicos de las CNN y ResNet. (https://d2l.ai/chapter_convolutional-neural-networks/index.html)
- CS231n: Convolutional Neural Networks for Visual Recognition (Stanford University): Material de clases sobre CNN. (http://cs231n.github.io/convolutional-networks/)
- Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift (Li et al., 2018): Artículo que explica los puntos a tener en cuenta al usar normalización por lotes y dropout juntos.
- Rethinking the Inception Architecture for Computer Vision (Szegedy et al., 2015): Explicación de Inception-v3 y los módulos inception. (https://arxiv.org/abs/1512.00567)
- Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex (Hubel & Wiesel, 1962): estudio sobre el córtex visual del gato. Artículo que inspiró el concepto de campo receptivo en las CNN. (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1359523/) 2. The Scientist and Engineer’s Guide to Digital Signal Processing (Steven W. Smith): libro que explica los principios básicos del procesamiento de señales digitales. Ayuda a comprender la convolución y los filtros. (http://www.dspguide.com/pdfbook.htm) 3. Gradient-based learning applied to document recognition (LeCun et al., 1998): reconocimiento de caracteres utilizando CNN. Introducción de LeNet-5. (http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf) 4. Deep Residual Learning for Image Recognition (He et al., 2015): artículo original de ResNet. (https://arxiv.org/pdf/1512.03385.pdf) 5. Network in Network (Lin et al., 2013): artículo que presenta la idea de convoluciones de 1x1. (https://arxiv.org/pdf/1312.4400.pdf) 6. Very Deep Convolutional Networks for Large-Scale Image Recognition (Simonyan & Zisserman, 2014): artículo de VGGNet. (https://arxiv.org/pdf/1409.1557.pdf) 7. Dive into Deep Learning (Zhang et al., 2023): en el capítulo 9 “Convolutional Neural Networks” se explican los conceptos básicos de las CNN y ResNet. (https://d2l.ai/chapter_convolutional-neural-networks/index.html) 8. CS231n: Convolutional Neural Networks for Visual Recognition (Stanford University): materiales de la clase sobre CNN. (http://cs231n.github.io/convolutional-networks/) 9. Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift (Li et al., 2018): artículo que explica los puntos a tener en cuenta al usar dropout y normalización por lotes juntos. 10. Rethinking the Inception Architecture for Computer Vision (Szegedy et al., 2015): explicación de Inception-v3 y los módulos inception. Traducción:
El aprendizaje profundo con funciones de activación no saturadas ha demostrado ser muy eficaz en una variedad de tareas, desde el reconocimiento de voz hasta la visión por computadora y las traducciones de lenguajes. En este artículo, proponemos una nueva estructura para las redes neuronales recurrentes (RNN) que utiliza funciones de activación no saturadas y permite un entrenamiento más eficiente.
| Característica | Descripción |
|---|---|
| Arquitectura | La arquitectura propuesta se basa en celdas RNN estandarizadas con funciones de activación no lineales. |
| Función de Activación | Se utiliza la función ReLU (Rectified Linear Unit) para evitar el problema del desvanecimiento del gradiente. |
| Ventajas | Mejora la eficiencia del entrenamiento y la capacidad de modelar secuencias largas. |
| Resultados | Los experimentos muestran un rendimiento superior en tareas de procesamiento de lenguaje natural y reconocimiento de voz. |
Esperamos que esta estructura propuesta contribuya al desarrollo de modelos RNN más robustos y eficientes.